∇²DFT — a new dataset and benchmark for solving quantum chemistry problems using neural networks

In this post, I will talk about our new dataset of small molecules in medicinal chemistry and a benchmark of graph neural models, which we collected through the efforts of a large team of researchers from the "Deep Learning in Life Sciences" and "Applied NLP" groups at AIRI, EPFL, SPbU, ISP RAS, and POMI RAS. In addition to creating a dataset of quantum chemical properties of 220 terabytes, we evaluated how well modern neural models solve the tasks of predicting energies and atomic forces, optimizing energy, and predicting Hamiltonians. Our research was accepted at the NeurIPS 2024 conference in the Datasets and Benchmarks track.

Happy reading!

About the Schrödinger Equation: What It Is and Why It Is Needed

Predicting the properties of molecules is an important step in creating a new drug, substance, or material. Testing new hypotheses in chemistry requires a significant amount of resources: the synthesis and further testing of the properties of the final substance can be long and expensive. Instead of conducting costly experiments, some properties can be assessed using quantum chemistry methods.

The behavior of systems at the quantum level is governed by an equation named after one of the founders of quantum mechanics, Erwin Schrödinger. It looks like this:

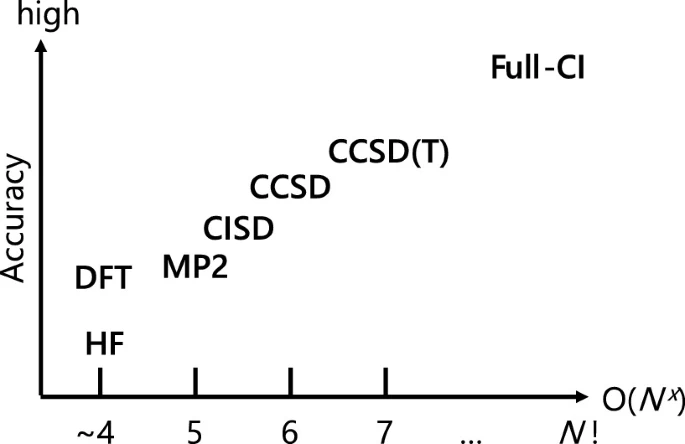
As can be seen from the graphs, the method based on density functional theory (DFT) is currently the optimal choice between simulation accuracy and the required amount of resources.

A few words about DFT

DFT is a mean-field method in which the many-particle problem is divided into several single-particle problems and which solves the Schrödinger equation for a single electron in the effective field of other electrons. The main difference between this method and more accurate ones is that it operates not with a many-particle wave function, but with an electron density, which is an observable quantity.

DFT allows considering systems on the scale of 1000 electrons with satisfactory accuracy (about 10 kcal/mol), thereby scaling up to systems that are already nano-objects, such as nanotubes, pieces of proteins, or parts of catalytic surfaces. The error of DFT is determined by the exchange-correlation functional, which is a compromise between accuracy and complexity. By selecting a good functional, the DFT error can be reduced to 1 kcal/mol, making it one of the most accurate methods.

Despite the relative simplicity of the DFT approach compared to more accurate ones (Quantum Monte Carlo and Coupled Clusters), it is still poorly applicable for daily calculation of large sets of molecules due to its computational cost. In this regard, scientists have begun to apply machine learning models to approximate the properties of new structures based on those calculated with its help.

Calculating quantum properties using neural networks

There are many approaches in machine learning, and in recent years they have been used in quantum chemistry in one way or another. But in the task of predicting the properties of molecules, neural network methods perform best.

In the 2017 paper Neural Message Passing for Quantum Chemistry, a way to solve this problem was proposed by representing a molecule as a graph, seasoned with a message passing algorithm. The new framework allowed achieving SOTA results in the task of predicting quantum chemical properties on the QM9 dataset (to be precise, the approach itself was proposed much earlier (for example, here), but it was in this paper that it was successfully applied to the task of molecular modeling).

In the future, this approach was improved, and new architectures for evaluating molecular properties (SchNet, DimeNet, PaiNN, Equiformer, NequIP, Allegro, MACE, etc.) appeared, using 3D information about the molecule (atom coordinates) instead of or together with the number and type of bonds.

One of the disadvantages of using such approaches is the need to train your model for each property. Transfer and multi-task learning methods are applicable in such tasks, but they significantly complicate the process.

Instead, you can use the so-called ab initio approach, when the model predicts some basic property, from the value of which all quantities of interest to the researcher can be calculated. Such properties can be the many-electron wave function, the electron density function, or the DFT Hamiltonian matrix. More information can be found, for example, in Frank Jensen's book Introduction to Computational Chemistry.

The current SOTA here is the approach with direct prediction of the wave function by the variational Monte Carlo method, proposed in the works on the architectures FermiNet and PauliNet. Neural network methods allow obtaining results qualitatively better than classical methods, but unfortunately, they do not significantly outperform the same DFT in terms of application speed, and at the same time require rather complex training.

The second approach uses the prediction of electron density, but it is complicated by the need to somehow represent it (for example, in the form of a functional basis expansion or using a graph neural network), as well as to compare functions on the grid. This approach is being developed by several research groups, for example, Peter Bjorn Jorgensen from the Technical University of Denmark and Jian Peng from the University of Illinois.

Finally, the third approach boils down to approximating the Hamiltonian matrix, which makes the problem conditionally discrete but leaves the attachment to the functional basis, plus the accuracy of this method is limited above by the accuracy of the DFT itself. The first works in this area were the models SchNOrb and PhiSNet. They allow obtaining Hamiltonian matrices and energy values close to reference ones, as well as accelerating the convergence of DFT algorithms. The main disadvantage of these approaches is their applicability only to one molecular formula, that is, such models generalize only to new geometries of the same molecule.

∇²DFT — dataset and benchmark

Our team likes the approach based on the approximation of Hamiltonian matrices, so one of the goals of our research was to develop such DFT prediction methods. We created a large dataset with various molecules and their calculated quantum chemical properties, called ∇²DFT (and its first and smaller version was called ∇DFT). Based on the resulting dataset, we made a benchmark of three types of tasks: predicting Hamiltonian matrices, predicting energy and atomic forces, and optimizing the geometry of the molecule (conformation).

The dataset preparation process consisted of 5 parts:

1. For each molecule from the dataset of drug-like compounds (MOSES), we generated up to 100 spatial geometries (conformations) using the ETKDG method.

2. Conformations for each molecule were clustered by distance between geometries using the Butina method. For clusters covering 99% of all conformations, we selected centroids, which make up the final dataset.

3. For each of the obtained geometries, we calculated electronic properties using the open quantum chemistry library Psi4 with the Kohn-Sham DFT method with the ωB97X-D potential and the def2-SVP basis set.

4. The final dataset was divided into training/test subsets in several ways to investigate the generalization ability of the methods. Specifically: training sets of different sizes (2,000, 5,000, 10,000, 100,000, and 700,000), test sets of conformations of the same structures present in the training sets, a test set of molecules not present in the training, and a test set of molecules whose main substructure (scaffold) is not found in the training sets.

5. For approximately 60,000 conformations, DFT relaxations (energy optimization processes) were run and the full trajectories of these processes were saved.

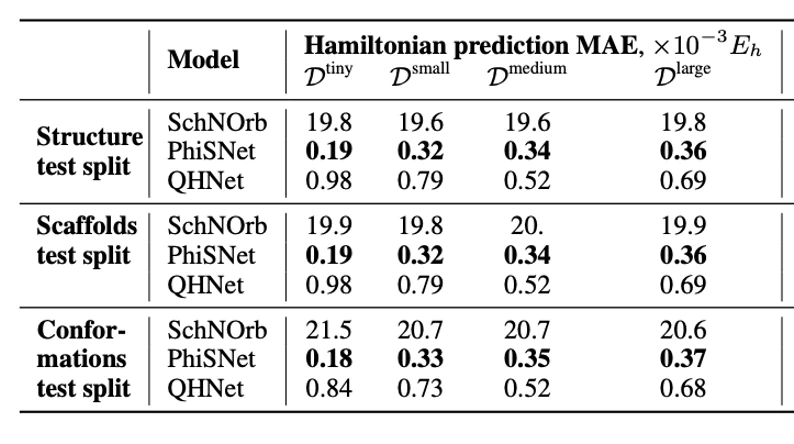
For the task of predicting Hamiltonian matrices, we generalized the code of the SchNOrb and PhiSNet models to work with different molecules and measured their generalization ability. We also added a comparison with the QHNet model, which is also adapted to work with different molecular structures. The corresponding metrics can be seen in the table below:

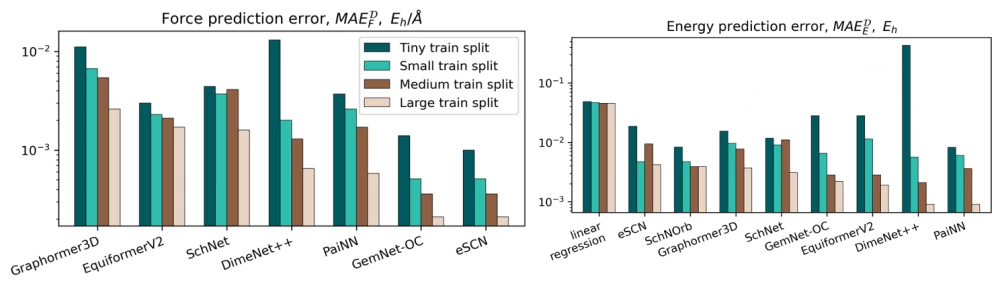
For the task of predicting energies and forces, we trained and compared 8 models based on graph neural networks (SchNet, PaiNN, DimeNet++, Graphormer3D, EquiformerV2, eSCN, and GemNet-OC). The corresponding metrics can be seen in the histograms below:

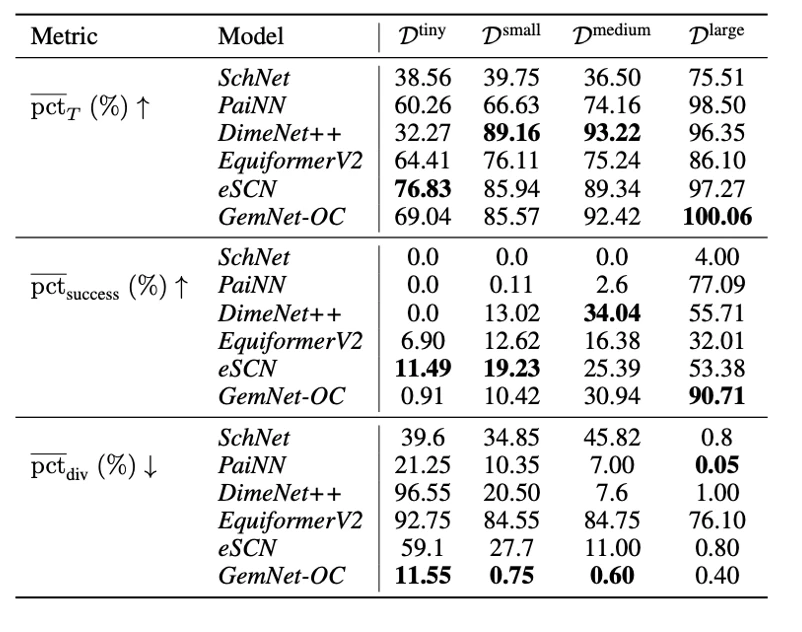
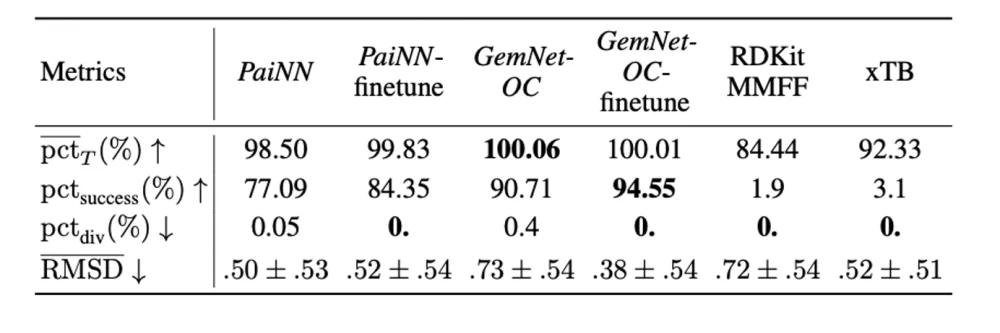
Finally, following our article, which we have already posted about on tekkix, we tested how well the models for predicting energies and forces can be applied to the independent search for optimal conformations (geometries with minimal energies). As can be seen in the tables below, the PaiNN and GemNet models, trained on large subsets of our dataset, perform the optimization task quite well. In addition, retraining on geometries from optimization trajectories leads to further improvement of the models.

As a result, with the support of colleagues from Skoltech and POMI RAS, we collected 15,716,667 conformations for 1,936,929 drug-like molecules, as well as their quantum properties, and made the database with a total size of about 220 terabytes publicly available on the Cloud platform. In addition to the data, we included 10 models for predicting the energy and atomic forces of molecular conformation and 3 models for working with density functional theory. The full dataset and examples of working with it are available through GitHub, and the analysis results are available in the articles: about ∇DFT and about ∇²DFT.

Conclusion

With our dataset, it can be seen that modern neural network models predict energies and forces quite well — at the level of accuracy of traditional quantum chemical methods, and also note their generalizing ability when tested on new molecules.

However, despite the fact that modern models for predicting Hamiltonians can speed up quantum chemical calculations by more than 3 orders of magnitude in time, their training remains a difficult task: it requires a large number of GPU hours (several GPU months on modern cards in the case of our dataset), and the process itself becomes much more complicated with increasing size and composition of molecules.

Our project continues to evolve, so subscribe and stay tuned for updates. We will be happy to receive your comments and pull requests!