Small numbers, big opportunities: how floating point accelerates AI and technology

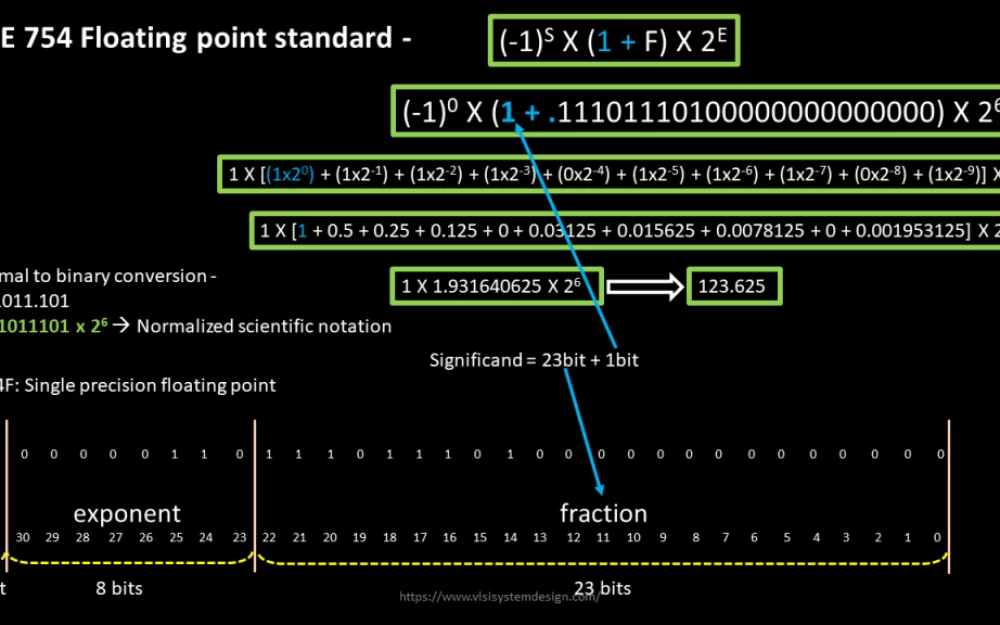
IEEE 754 Standard

At the very beginning of the computer era, floating-point operations were a real challenge for programmers and engineers. The lack of a unified standard meant that each system could interpret such numbers in its own way. This created huge problems when transferring programs between different platforms and often led to unpredictable calculation results.
In 1985, the situation changed with the adoption of the IEEE 754 standard. This standard became the foundation for the representation and processing of floating-point numbers in most modern computing systems. It defined the format for representing numbers, including elements such as sign, exponent, and mantissa, and also established rules for rounding and handling exceptional situations.
Before the IEEE 754 standard, floating-point operations were performed in software, which was extremely inefficient. Some systems had hardware modules for these operations, but they were not compatible with each other. The standard allowed for a unified approach to working with floating-point numbers and significantly simplified the lives of developers.

The emergence of hardware support

After the approval of the IEEE 754 standard, processor manufacturers began actively implementing hardware support for floating-point operations. Mathematical coprocessors, such as the Intel 8087, appeared, which worked in tandem with the main CPU and accelerated calculations by tens of times.
Soon, the functions of coprocessors were integrated directly into central processors. For example, starting with the Intel 486DX, the FPU (Floating Point Unit) became an integral part of the CPU. This allowed complex mathematical operations to be performed faster and more efficiently, paving the way for the development of graphics, scientific computing, and many other fields.
Modern processors are equipped with powerful FPUs that support various floating-point number formats and can perform billions of operations per second. Additionally, vector instructions such as SSE, AVX, and AVX-512 have been developed, allowing operations on multiple numbers simultaneously, significantly increasing performance.

Floating Point in GPU

Graphics Processing Units (GPUs) were originally designed to accelerate graphics rendering, where floating-point operations play a key role. Their architecture is oriented towards massive parallelism, allowing thousands and even millions of operations to be performed simultaneously.
With the development of technology, GPUs have been used not only for graphics but also for general-purpose computing on Graphics Processing Units (GPGPU). Programming languages such as CUDA from NVIDIA and OpenCL from the Khronos Group have opened up GPU power for solving various tasks, including scientific calculations, modeling, and, of course, neural network training.
One of the key factors in GPU efficiency is the support for various floating-point formats, including small formats such as FP16 (16-bit half-precision) and even INT8 (8-bit integers). This allows for optimized computations, reducing power consumption and increasing data processing speed.

Calculation accuracy and the role of quantization in AI

In today's world, artificial intelligence and neural networks have become key elements of many technologies. Processing large amounts of data and complex models requires significant computational resources. Various methods are used to optimize the performance of such systems, including the use of reduced precision numbers and hardware-accelerated computations, which allow for efficient information processing and acceleration of various processes.

Number precision

Numbers can be represented with different precision. For example, FP32 (32-bit floating-point representation) allows for very precise storage of real numbers, which is critically important for training models where high precision is required for proper weight adjustment.
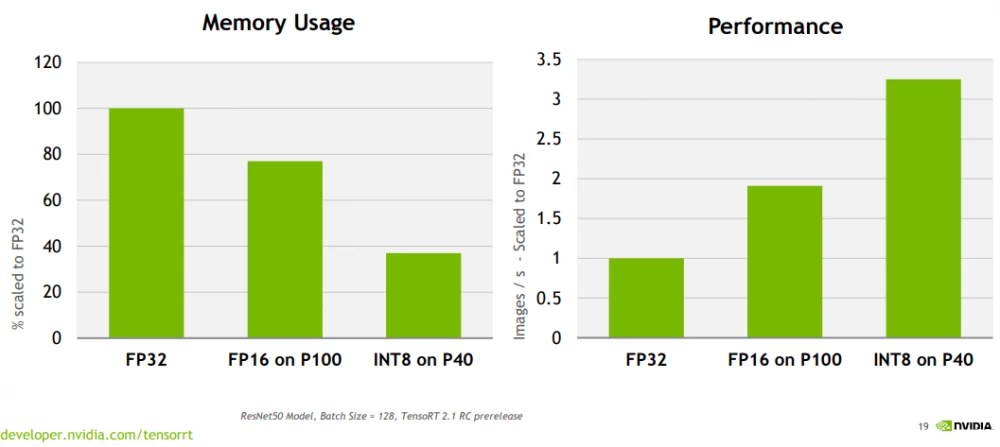
However, in subsequent stages, as well as during usage, such precision may be excessive as it increases the amount of memory used and negatively affects computation time. To optimize the AI training process, FP16 (16-bit floating-point representation) can be used, which is an intermediate option but retains sufficient precision for most tasks.
In most "everyday" tasks, when the model is already trained, it is reasonable to use less precise representations of numbers, such as INT8 (8-bit integers). Using such numbers helps process most requests without loss of model quality, especially in speech and text processing tasks.

Neural Network Quantization

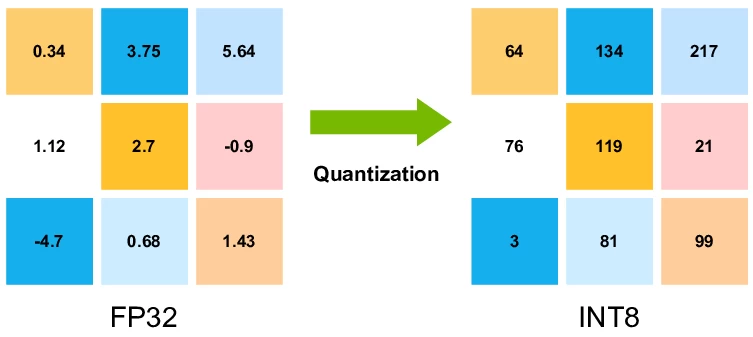
Quantization is the process of converting numbers from more precise formats (e.g., FP32) to less precise ones (e.g., INT8). The main idea is that quantization can significantly reduce computation and memory consumption with minimal impact on result quality.

Let's briefly consider the process itself:

1. Compression of values, that is, instead of an exact representation of all decimal places used in the floating-point format, the number is rounded to the nearest integer that can be represented in the new format.

2. Scale and shift: the scale determines how much the original numbers will be "stretched" or "compressed" to fit the new range, and the zero-point allows negative and positive numbers to be correctly displayed by shifting the range of values.

Visually for us, it looks like a picture that we see in a 32-bit format, but we reduced the color settings to 128 shades. We simplified the image, but the picture remained recognizable.

Architectures optimized for AI

Hardware manufacturers are actively developing solutions specifically designed for artificial intelligence and machine learning tasks.

Nvidia and their graphics accelerators

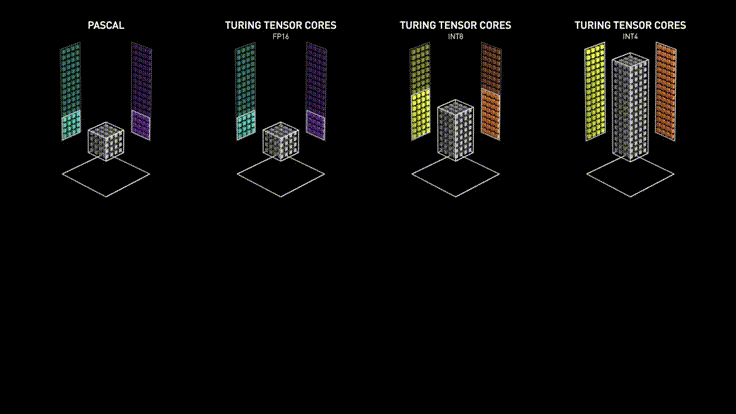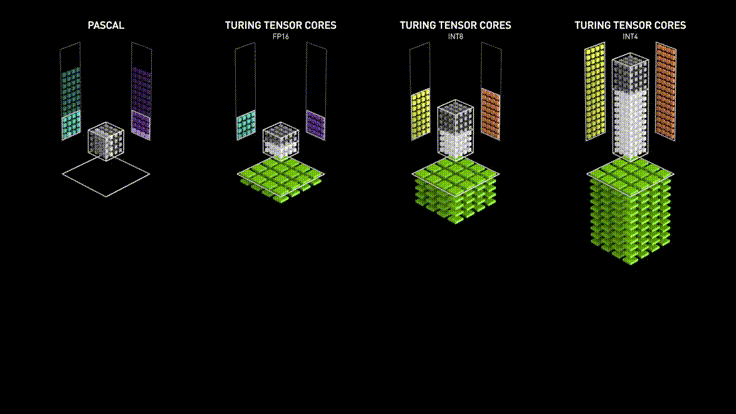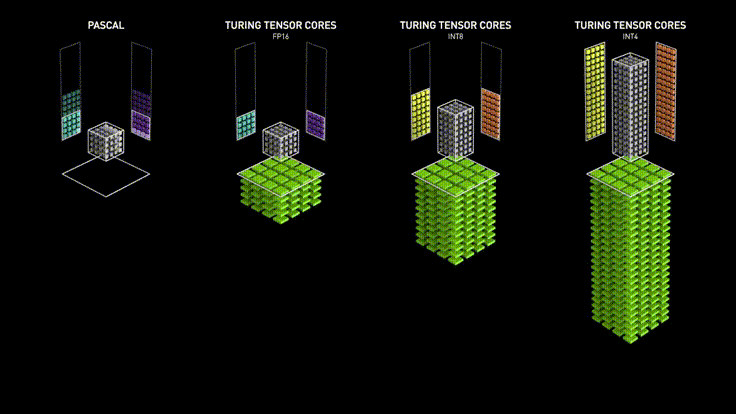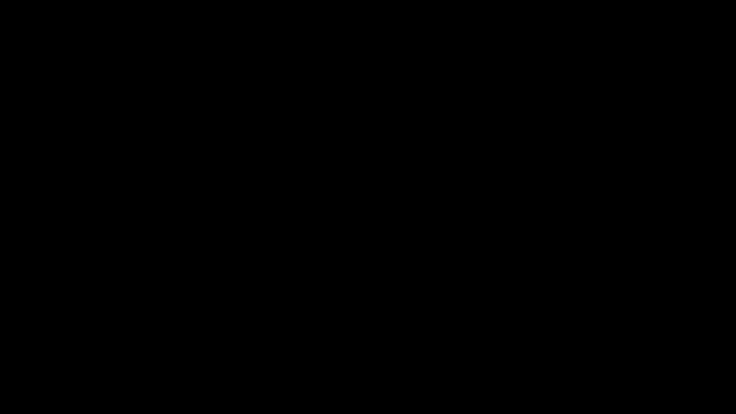
The Nvidia Corporation pays great attention to the development of GPUs optimized for AI training and inference. The success of their accelerators is largely ensured by specialized tensor cores that significantly speed up working with floating-point numbers, as well as careful software support for their products. For a better understanding, let's note a few features of Nvidia accelerators:

• Advanced tensor cores that accelerate various computation modes: BF16, TF16, FP32, and others;

• Specialized architectures aimed at AI work: Blackwell, Hooper, Volta;

• High energy efficiency, reducing electricity costs and heat generation.

Other companies and solutions

• AMD: develops solutions for AI and HPC. Radeon Instinct accelerators with matrix cores speed up machine learning tasks. The AMD Instinct MI300X series on the CDNA™ 3 architecture supports formats from INT8 to FP64, providing high performance and energy efficiency.

• Google: developed specialized TPU (Tensor Processing Unit) processors optimized for working with Bfloat16 and INT8 formats.

• Ampere Computing: produces unique ARM processors with built-in 128-bit vector blocks that efficiently perform linear algebra operations, which are the basis of most machine learning algorithms.

• Intel: integrates technologies to accelerate low-precision operations into its processors, such as Intel DL Boost. In addition, Intel offers specialized Gaudi accelerators for accelerating AI training and inference, as well as Intel GPU Max graphics processors, which can be an excellent solution for high-performance computing.

Practical application of small numbers

The use of small floating-point numbers has wide practical applications in various fields.

Mobile Devices and Embedded Systems

Limited resources of mobile devices require efficient use of memory and energy. Model quantization allows complex neural networks to run on smartphones, tablets, and IoT devices, providing speech recognition, image processing, and other AI services.

Cloud Services and Data Centers

In large data centers, reducing power consumption and increasing computing density are key tasks. The use of processors and accelerators optimized for small numbers allows more data to be processed with less cost.

Automotive Industry

Autonomous driving and driver assistance systems require processing huge amounts of data in real-time. Optimizing computations with small numbers provides the necessary speed and efficiency.

The Future of Small Floating-Point Numbers

Technology continues to evolve, and we can expect new formats and methods of data processing to emerge.

• New data formats: the emergence of even more efficient number formats, such as Posit, which promise to improve accuracy and performance.

• Hardware innovations: the development of quantum computing and neuromorphic chips may change the approach to information processing.

• Algorithmic improvements: new training and optimization methods may allow the use of even lower precision levels without compromising model quality.

Conclusion

Floating-point numbers are not just a mathematical abstraction, but a key tool in modern computing. Different formats of these numbers allow adaptation to the specific requirements of tasks, finding a balance between accuracy, speed, and efficiency.
Have you ever had to use optimization involving floating-point numbers in your tasks, or perhaps even design a new structure for storing some specific data of a particular volume or precision? It would be interesting to read in the comments and thank you for reading!