- AI
- A
Atlas: How to reconstruct a 3D scene from a set of images
Hello everyone! If you are interested in 3D technologies or just want to learn more about modern methods of creating three-dimensional models, you should definitely read this article. We will dive into the Atlas method - a unique way of 3D scene reconstruction based on only 2D images. You will learn how linear regression and truncated signed distance function can significantly simplify the modeling process, providing more accurate results without the need for depth maps.
Hello everyone, in this article we will analyze the method called Atlas, what it represents, consider the main concepts and principle of operation.
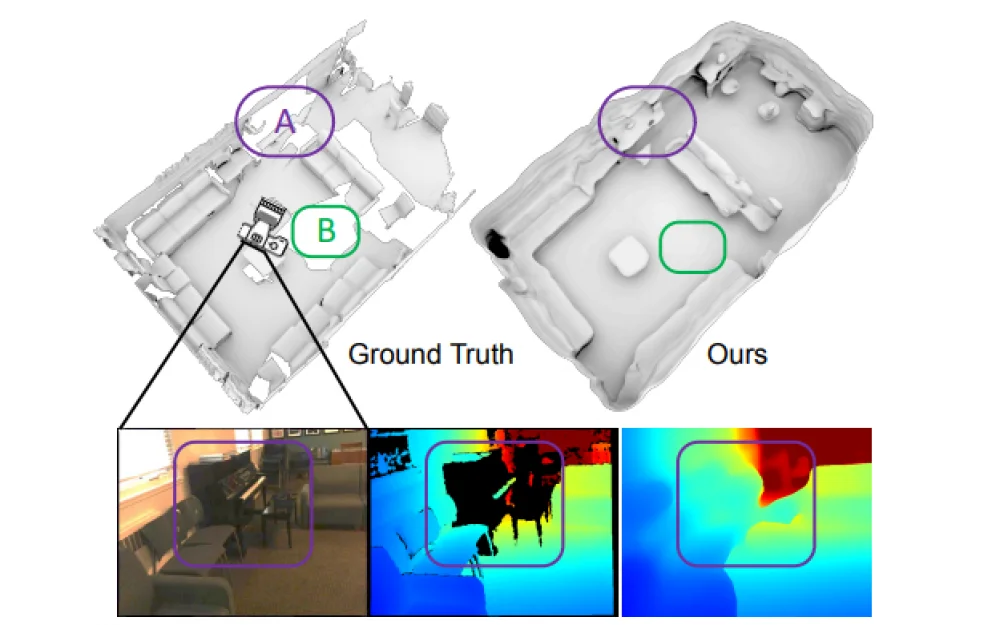
I present the method of 3D scene reconstruction (the process of creating a three-dimensional model of an object based on two-dimensional images or video), which is based on linear regression, truncated signed distance function (TSDF) (We will consider in the next section) from a set of RGB images with given positions (for each image, the camera parameters are known, including its position and orientation in space). Usually, 3D reconstruction approaches rely on depth maps before evaluating the 3D scene. We assume that direct regression in 3D is more efficient. 2D-CNN extracts features from each image independently, which are then projected and accumulated in the voxel volume using internal (Focal length, Projection center, Distortion coefficients) and external (Position, Orientation) camera parameters. After that, 3D-CNN refines the accumulated features and predicts TSDF values.
TSDF
If you are familiar with this principle, you can skip this section and go to the main part of the article. If not, then here is TSDF (Truncated Signed Distance Function). However, before discussing it, let's talk about SDF (Signed Distance Function). First of all, it is a function that describes the distance from a point to a certain surface or object in three-dimensional space.
Let's denote:
If the point is inside the object, the function assigns a positive value, and a negative value if it is outside.
Alright, we have figured this out, but we have TSDF, which does not complicate the task too much, because we just cut off part of the data, and let's say it works in the range [-1;1]
Where sng(x) is the sign function:
Introduction
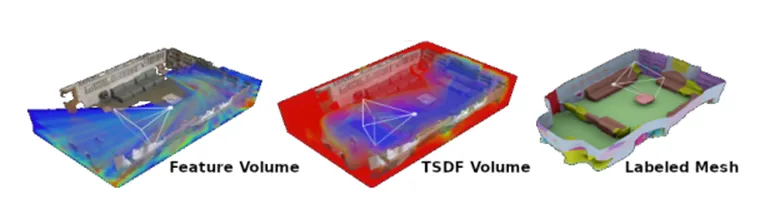
The figure shows a graphical representation of the data processing method. On the left is the Feature Volume, where features from images are projected and accumulated into the volume. In the middle is the TSDF Volume, which goes through a refinement process using a 3D CNN (convolutional neural network). On the right is the Labeled Mesh, created based on TSDF, which can also contain semantic labels. The figure illustrates the sequence of data processing from features to the final model.
In this work, we note that depth maps are often intermediate representations that are then merged with other depth maps into a complete 3D model. In this regard, we propose a method that takes a sequence of RGB images and directly predicts a complete 3D model in a trainable end-to-end manner (the model is trained simultaneously, without splitting into separate stages from start to finish). This allows the network to combine more information and better learn geometric priorities about the world, leading to significantly better reconstructions. Moreover, it reduces system complexity by eliminating stages such as frame selection and reduces the required computational costs by distributing them across the entire sequence.
The method is based on two main directions: multi-view stereo, based on cost volume (in short, we just create a depth map) and refinement of the truncated signed distance function (TSDF). Multi-view stereo uses cost volume with plane sweeping to create 3D models from 2D images taken at different angles. Here, the reference image (i.e., we will start from it) is deformed to the target image (i.e., we will change our reference image in every possible way to better match the shape and angles of the target image) for each of the fixed set of depth planes and accumulated into a 3D cost volume. Depth is computed by taking the argument of the minimum over the planes. This procedure is made more robust by extracting image features using CNN and filtering the cost volume using another CNN before taking the argument of the minimum.
TSDF refinement starts by merging depth maps from the depth sensor into an initial voxel volume using TSDF fusion, where each voxel stores the truncated signed distance to the nearest surface. Note that from this implicit representation, a triangulated mesh can be extracted by finding the zero-crossing surface (object boundary detection) using the marching cubes algorithm. TSDF refinement methods take this noisy and incomplete TSDF as input and refine it by passing it through a 3D convolutional encoder-decoder network.
Method
Our method takes as input a sequence of RGB images of arbitrary length, each with known camera parameters and position. These images pass through a 2D CNN to extract features. The features are then projected into a 3D voxel volume and accumulated using a sliding average. Once the image features have been combined in 3D, we regress the TSDF directly using a 3D CNN (see figure). We also experiment with adding an additional output layer to predict semantic segmentation.
Green blocks: These blocks represent strided convolutions with a stride of 2, used to reduce the resolution of the data.
Red blocks: These blocks denote trilinear upsampling to increase the resolution of the data.
Arrows: They indicate skip connections from the encoder to the decoder, allowing information to be passed from earlier layers to deeper layers.
Images: They show intermediate outputs obtained at different stages of processing.
The network architecture assumes that TSDF (Truncated Signed Distance Function) predictions occur at various levels of resolution, starting from coarser and refining at a finer stage.
At each decoding stage, intermediate output layers are added before upscaling. These outputs help control the learning process and improve predictions near surfaces. Voxels predicted beyond 0.99 of the set distance are clamped to one. Network parameter updates occur only for voxels that are not clamped, helping to avoid the influence of empty voxels at higher resolutions and improving learning quality.
Implementation details
To implement our method, we use ResNet50-FPN, followed by a merging method with 32 output channels as our 2D backbone. Our 3D CNN consists of a resolution pyramid with four levels (i.e., we divide our image (640x480) into 4 levels, where each subsequent level is half the resolution of the previous level (i.e., level 2 will have dimensions 320x240, and so on)), where we double the number of channels each time we reduce the resolution. The encoder consists of (1, 2, 3, 4) residual blocks at each level, and the decoder consists of (3, 2, 1) residual blocks.
Controlling multi-scale TSDF reconstructions is done using L1 losses relative to the true TSDF values. Predicted and target values are logarithmized before applying L1 losses, with backpropagation losses calculated only for observed vectors. A penalty is also introduced for voxels with a fully vertical column equal to 1 to exclude artifacts behind walls.
To build true TSDF values, TSDF merging is performed at each resolution before training. The network is trained using 50 randomly selected images from the full sequence. A voxel size of 4 cm³ is used with a grid of 160×160×64, corresponding to a volume of 6.4 × 6.4 × 2.56 meters. During testing, feature volumes are accumulated, allowing for working with sequences of arbitrary length.
In conclusion.
In conclusion, I want to say that the Atlas method is indeed a very good method, which includes such advantages as high accuracy (due to the previously known shapes), and the method also copes well with the reconstruction of complex objects. However, like any method, this one also has its drawbacks. First of all, it requires very well-labeled data. Also, considering that improvements in speed were invested in this method, the method may still require significant computational resources.
Therefore, if you have the opportunity to provide the necessary conditions and equipment, this method will fit perfectly into the tools for implementing your ideas.
That's all, thank you all for reading the article, I hope it helped you!
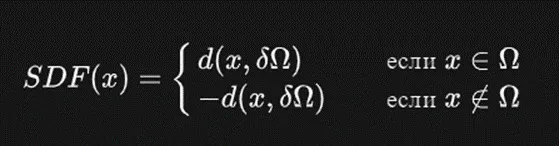
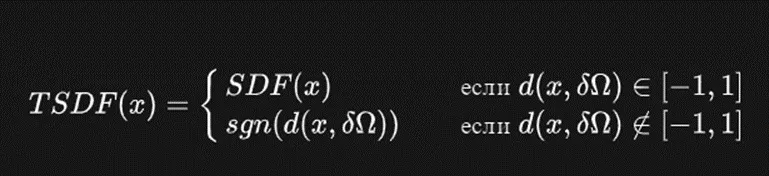
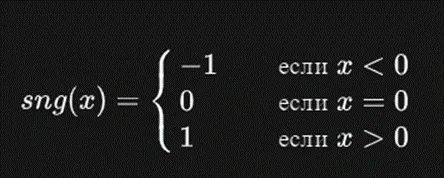











Write comment