- AI
- A
About the peel of the hyperorange
When you unexpectedly take on some task, it can touch some deep layers of the universe and a slightly rusty mechanism comes into motion, showing in the windows amazing combinations of symbols, not seen or recognized before.
Preamble
Having been bogged down in an endless review of a thick monograph on deep learning, at some point I wrote this note, but then I discovered that the hyperorange peel had already been mentioned on tekkix in an article on Bayesian inference, albeit in a different context. Nevertheless, this note settled in the drafts. But now, having written a large review and after editing it will be published literally in a few days, I thought that I would also publish this note. Well, what do I risk, at worst they will expose and expel me.
Here it is, this note.
On the problem of test data density for AI models
For example, last year I took up translating a monograph on machine learning in the Deep Learning version. Nothing foreshadowed, just in the eighth chapter they discussed why well-trained models on test data do not behave so well, and the discussion on the example of the multidimensional classification problem led the author to lament that the higher the dimensionality of the problem, the more sparse the test data becomes. A sample of 100,000 samples looks decent in a three-dimensional problem, but as soon as the dimensionality of the problem begins to grow, the density of samples in the input/output pair space drops catastrophically. To explain his thought, the author talks about what I knew in infancy when I read the journal "Quantum" and dreamed of entering MIPT, but since then I have completely forgotten.
The example is very simple, but illustrative, do not disdain elementary mathematics. Let's take a circle inscribed in a square with a side equal to one. What will be the area of the circle? The answer is known from the school mathematics course:
That is, the area of the circle inscribed in the square eats up 0.79 of the area of this square.
We increase the dimension by one. We inscribe a sphere in a cube. The same school calculations show that the sphere eats up from the volume of the cube into which it is inscribed only about 0.5235:
When the dimensionality of the hypercube grows, this ratio decreases catastrophically and tends to zero. Now ask yourself - why on earth does the volume of a multidimensional hypercube remain one, while the volume of the sphere inscribed in it shrinks? Moreover, sample points that seemed to be uniformly distributed in two-dimensional and three-dimensional space begin to stick to the surface of the hypersphere (the well-known saying that the main volume of a hyper-orange is concentrated in its peel, not in its pulp, is quite a Zen observation).
On packing spheres in multidimensional space
Well, during the day, while translating the eighth chapter, I was surprised by this and only that. But then at night I wake up, as usually happens during a five-point magnetic storm, and start browsing the electric internet. And there I find news that I missed by two and a half months (at the time of the described events). News from July 5, 2023. Mathematician Maryna Viazovska was awarded the Fields Medal (the Nobel Prize for mathematicians, so to speak). She became the second woman to receive it after the Persian Maryam Mirzakhani, who received it in 2014, and in 2017, at the age of 40, passed away from breast cancer.
Maryna Viazovska, thank God, is alive and well, heads the chair of arithmetic at the Polytechnic School in Lausanne, where she lives with her husband and two children.
My reaction to this news is explained not by the fact that she is a woman, but by what she was awarded for. For solving the problem of the densest packing of spheres in multidimensional space. I first learned about this problem from my childhood friend, who became rich and famous after moving from a provincial town in Russia to the capital city of Tel Aviv. It turned out that this purely mathematical problem has applications in the theory of error-correcting codes, where my childhood friend achieved significant results that formed the basis of his scientific career as a professor at Tel Aviv University. I remember many years ago, my friend joked that so few people were working on this problem that it was appropriate to start another article with an improved estimate of the density of sphere packing in multidimensional space with the words "Dear John and Pete".
So, it turned out that since those distant times when my childhood friend was working on this problem, many mathematicians have struggled with it, but to no avail. But Maryna Viazovska turned out to be more persistent than others and published the solution to this problem for dimension 8 and (with a number of co-authors) for dimension 24. It turned out that in these two dimensions, everything is completely different from other dimensions. And no one knows why! Moreover, a Pandora's box of applications of this discovery has opened, and it seems that this will be at least as significant as the application for the theory of error-correcting codes.
Many prominent mathematicians, after reading Maryna Viazovska's 23-page proof, said that they do not expect to see anything more beautiful in their lives. For reference, the solution to this problem for dimension 3 (Kepler's conjecture) took about three hundred pages of text, so Maryna Viazovska's solution was called "astonishingly simple".
A hypersphere inscribed in a hypercube, in a simple problem of forming a representative sample of test data for training AI models, timidly joins this vast and boundless topic.
The breakthrough achieved by Maryna Viazovska is compared to the breakthroughs in mathematics of the 19th and 20th centuries.
Life blindly copies literature
As if there weren't enough coincidences in this story, I was also listening to the novel "The Three-Body Problem" by Chinese writer Liu Cixin, translated by Olga Glushkova from Ken Liu's English translation, while driving and cooking. There, essentially, the same story. A purely mathematical problem, which also has no analytical solution, is at the center of the plot about an extraterrestrial civilization that arose in the triple star system of Alpha Centauri, but cannot survive and perishes again and again simply because no one can solve the three-body problem.
It is assumed that the problem of the densest packing of spheres in three-dimensional space is historically associated with the practical problem of storing cannonballs, which gives it an even more sinister connotation in the current situation around the world.

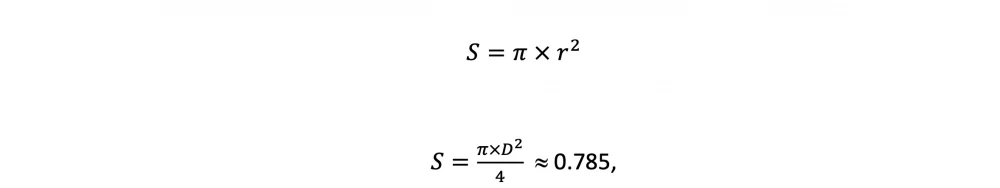
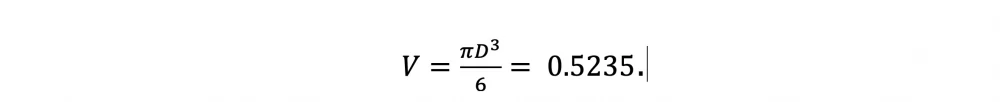









Write comment