- AI
- A
Fundamental mathematics — the theory of everything in IT and beyond. Type theory and formalization in Coq
We have 3 "theories of everything" - the scientific picture of the world (everything is reduced to the laws of physics), computer science (everything is reduced to bits), and the foundation of mathematics (everything is reduced to logic). It is the foundation of mathematics that is of particular interest, as it is the foundation for the other two foundations and has deep philosophical meaning.
For the past 2 years (2023-2024), I have been very interested in it and have done quite a lot of work on an in-depth study of type theory (Calculus of Constructions), and I am ready to share the results, as well as talk about nine areas where this can be applied in practice. A lot turned out better than I planned. Initially, the prospects were not very clear, and therefore I did not tell friends and colleagues about my work in this direction and called it the "Secret Project". But now that much has become clear and successful, I can share the success. Actually, in this article, I will tell you not only about the foundation of mathematics itself, but also its connection with the daily work of a programmer, as well as with Computer Science/Data Science and AI/ML. I will draw you a big and beautiful picture, where everything is clear and logically follows from a small set of type inference rules (11 pieces) and set theory axioms (9 pieces).
We have 3 foundations of mathematics - set theory (convenient for humans), type theory (convenient for computers), and category theory (I don't know why it is needed at all). They are roughly equal in power and one can be expressed within the other. Type theory is of particular interest because it can be easily programmed inside a computer and used as a strict foundation for other theories, which does not allow for errors and checks your every action.
And now I will tell you a short history of theorem provers (proof assistants) - these are programs that allow you to prove mathematical theorems and build the foundation of mathematics from scratch based on them. In 1973, the Mizar project (in Poland) appeared and it was the first successful theorem prover. At the moment, its library is the largest (52,000 proven theorems and 10,000 mathematical definitions).
The developers of Mizar tried to create a theorem prover entirely based on set theory (which seemed logical at the time), but in the end, it turned out to be a huge architectural crutch - they had to support 2 cores simultaneously (type theory and set theory) instead of one. This is bad not only for the development/maintenance of the system but also for learning/training/expansion.
Over time, type theory has formed as a separate discipline, well-developed and established. Researchers managed to very cleanly (without crutches) express mathematical logic within type theory and make it 100% compatible with how mathematicians think. How they managed to figure this out and make such a big breakthrough - I don't know. So, if we fully formalize mathematical logic, then axiomatic set theory is very cleanly and easily derived from it. It is only necessary to axiomatically define the existence of the membership relation to a set (∈), as well as add 9 ZFC axioms (Zermelo–Fraenkel Set Theory), which essentially postulate the existence of two sets (empty and infinite) and how to work with them. And the formal system of mathematical logic itself (a set of rules) is called Natural Deduction.
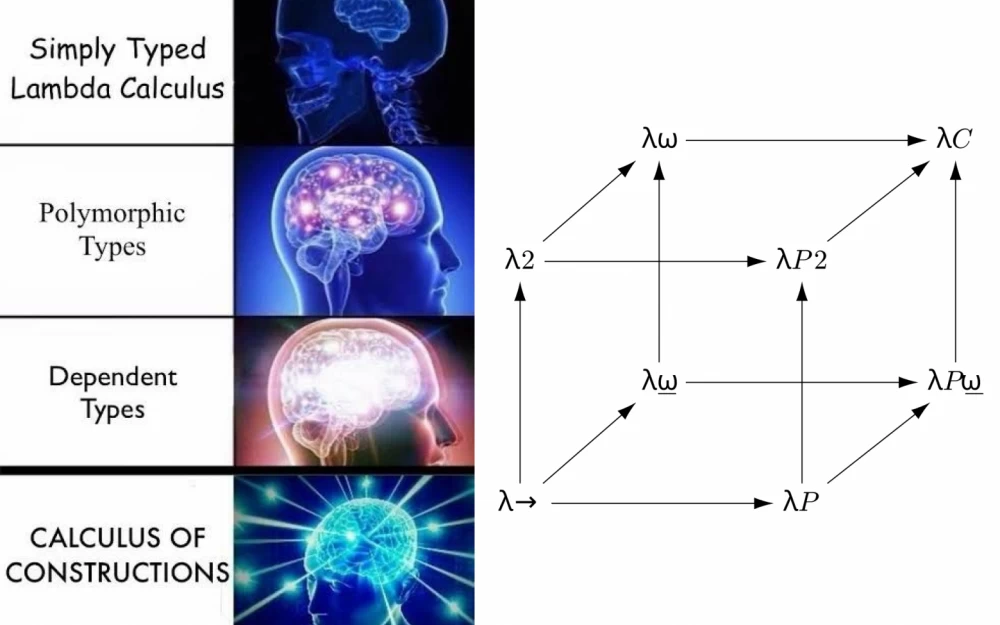
There are 2 popular type theories - Martin-Löf type theory (MLTT) and Calculus of Construction (CoC). They are roughly equal in power and have rather cultural/territorial differences. Nevertheless, Calculus of Construction is somewhat newer and more compact, and is used by the two most popular theorem provers in the industry - Coq and Lean. And there is also a super-quality and new textbook by Rob Nederpelt (Type Theory and Formal Proof: An Introduction). That's why I chose it.
Actually, 80% of my efforts to study the foundations of mathematics over the past two years have been built around this awesome book. The authors of the book did a tremendous job and analyzed 147 sources (other books and articles) to collect all the best in one place. Thanks to their work, I mastered this area in just 2 years instead of 10 years. I have solved almost the entire book and almost all the exercises, completely covering the first 13 chapters (300 pages) of the book. This book builds the foundation of mathematics from scratch and explains/formally introduces all concepts and notations. One of the interesting features of the book is that the author uses a modern constructive approach and expresses mathematical logic in a completely constructive way, without using a truth table even once. This is very good for learning and understanding, and also clearly shows how type theory can intertwine with mathematical logic and what many logical operations actually are at a low level.
The content of the book can be divided into 3 parts - in the first part (chapters 1 - 6) the author from scratch (from lambda calculus) gradually builds and complicates the type system and goes through the entire lambda cube to eventually get the golden classic - Calculus of Constructions (λC). In the second part (chapters 7 - 13) - the author explains how to fit mathematical logic and set theory into this type theory. In the third part (chapters 14 - 15) the author formalizes integers (Z) and their arithmetic within type theory, gives the basics of number theory, and also formalizes the proof of Bézout's theorem as a demonstration of the type system.
Actually, I solved chapters 1-7 on paper (with 100% coverage of all exercises at the end of the chapters), then I wrote a small mobile application for Android (MathConstructor) and covered chapters 5, 6, 7, and 11 in it. I covered chapters 11-13 already inside Coq, you can find the sources in my GitHub. And it turned out to be very cool, useful, and efficient! But I lacked the motivation for chapters 14-15, because in chapter 13 the author did not cover set theory very clearly. He decided to use a hybrid approach (with crutches to introduce many concepts of set theory into type theory, instead of purely deriving everything from ZFC axioms). I didn't like it at all and had to switch to another textbook on set theory.
Chapters of the book, their coverage, difficulty rating, and tools I used for learning
№ | Chapter | Difficulty | My coverage | I used | I recommend you |
1 | Untyped lambda calculus | 9 | 100% | Pen & Paper, Anki | Pen & Paper, Anki |
2 | Simply typed lambda calculus | 6 | 100% | Pen & Paper, Anki | Coq |
3 | Second order typed lambda calculus | 5 | 100% | Pen & Paper, Anki | Coq |
4 | Types dependent on types | 5 | 100% | Pen & Paper, Anki, Custom App | Coq |
5 | Types dependent on terms | 5 | 100% | Pen & Paper, Anki, Custom App | Coq |
6 | The Calculus of Constructions | 5 | 100% | Pen & Paper, Anki, Custom App | Coq |
7 | The encoding of logical notions in λC | 7 | 100% | Custom App | Coq |
8 | Definitions | 4 | 100% | Pen & Paper | Coq |
9 | Extension of λC with definitions | 5 | 100% | Pen & Paper | Coq |
10 | Rules and properties of λD | 5 | 100% | Pen & Paper | Coq |
11 | Flag-style natural deduction in λD | 7 | 100% | Custom App, Coq | Coq |
12 | Mathematics in λD: a first attempt | 6 | 100% | Coq | Coq |
13 | Sets and subsets | 7 | 100% | Coq | - |
14 | Numbers and arithmetic in λD | 8 |
Actually, I took an old and classic textbook on set theory from 1963 (Set theory and logic by Robert Stoll), and immediately jumped to Chapter 7 (Informal Axiomatic Set Theory), which provides the ZFC axioms and derives from them the set of natural numbers and its basic properties, and formalized about half of the chapter in a month. This was a test of the type theory and Coq for strength - and the test was successfully passed! I was amazed at how clearly the 1963 author explains everything. Even his strangest statements and mathematical constructions turned out to be very necessary and useful in formalization. All his steps, 100% of his thought process can be transferred 1-1 to the formal language of type theory. In general, I was lucky with the book again, although there are many technical typos, but they are not a problem. I am sure that I will return to this book again.
As a result, in just a month I managed to close a huge number of "gray areas" and gaps in understanding key mathematical concepts that I had formed in 2021 - 2022 while taking various standard math courses like Calculus I / II / III. I managed to prove the existence of the set of natural numbers (N) - to extract it from the axiom of infinity (ZF_Infinity), as well as derive 5 Peano axioms (on which all numerical systems are built), and also derive the principle of mathematical induction, and from it - derive the principle of strong induction. I also managed to derive the private axiom of choice (more convenient) from the general axiom of choice (ZF7_Choice), and from it (using Diaconescu's theorem) derive the axiom of the excluded middle, on which all non-constructive (classical) mathematics is based. And all this is very interesting and useful. Many axioms are no longer axioms for me, but are derived from the 9 ZFC axioms. I really like this approach. Perhaps I am close to the philosophy of logisticians and formalists.
As a result, based on these two books on type theory and set theory, I managed to lay the foundation of my own Coq library, which is written completely from scratch and which I understand 100% how it works from the inside. I thought for a long time about what to call it, and ChatGPT suggested the name ZFCFramework. So let's call it that. Actually, in the next couple of years, I plan to actively develop and expand it, apply it for various educational purposes. It's really cool that I now have such a tool. If I delve into different branches of mathematics and take new courses, I can simultaneously formalize them in Coq and strengthen the foundation, as well as get the maximum output and the deepest result from the efforts spent on courses or textbooks.
Regarding my mobile Android application MathConstructor: I haven't posted it anywhere yet, but I plan to post it somewhere in 2025 along with all the source codes, and there will be a separate article for this. But you don't have to wait - you can develop your own analogue - and it's not difficult at all! It took me only 4 days to develop a working Calculus of Constructions, and chapters 5-6-7 were almost completely covered. It took another two weeks for bug fixes, various conveniences, and refining λC to λD. As Knuth said, "The best way to understand something thoroughly is to try to teach it to a computer." Developing an application from scratch will give you 100% understanding of the material, and if you use my application - only 90-95%. Take the Euler font and any HTML engine, and this is enough to present any material from the book.
If you are smart and brave enough, you can immediately jump to chapter 11 in the book on type theory and program mathematical logic/solve logical problems within Coq, and return to previous chapters as questions arise. And use my sources, in which I have 100% formalized all the content of the chapter and all the exercises at the end of the chapter, for reference and when difficulties arise. I got 700 lines of code, which is not a lot. It should also be noted here that I completely disabled the standard Coq library (option '-noinit'), and also did not use inductive types, which are very popular in the community of Coq-loving mathematicians.
As for the first chapter, it is quite capacious and gives the basics of lambda calculus. It is highly desirable to solve it on paper if you have no experience with lambda calculus theory. Coq is not compatible with Untyped lambda calculus, so it cannot be used for self-testing. If you know an environment (or programming language) that is compatible with untyped lambda calculus and will allow you to formalize the content of the chapter in them and perform calculations/checks, be sure to write about it in the comments. If you can solve the first chapter in such an environment, be sure to post the sources and send me a link. I wouldn't mind going back to the first chapter and reviewing the material.
As for the axiomatic set theory (ZFC), it has many advantages and there is a strong motivation for mastering it. ZFC appeared 100 years ago and over the course of a century all branches of mathematics were rooted in it. Any classic math textbook can be reduced to it 1-1, even if it is not explicitly referenced. Of course, there are other set theories. For example, the Mizar project uses the Tarski-Grothendieck set theory (TG), and it is slightly stronger than ZFC. But I have not yet come across real cases where ZFC was not enough.
If you want a short series of introductory lectures on ZFC, I can recommend you Richard Borcherds' playlist on YouTube. He is one of the coolest mathematicians in the world, received the Fields Medal in 1998 — one of the most prestigious awards in mathematics (it is often called the "Nobel Prize for mathematicians"). Richard recorded a free series of 8 video lessons and covered all the ZFC axioms quite clearly and concisely. I watched and took notes on it in 2023 in a week and a half.
Mathematics is often divided into 2 types - computational (finding derivatives\solving equations and so on), and axiomatic (proof-based/rigorous). The second type is the "real" mathematics. You can read about mathematical maturity (Mathematical maturity) and type theory just helps to achieve it guaranteed. Terence Tao suggested dividing mathematical education into 3 stages - Pre-rigorous/Rigorous/Post-rigorous. Actually, the formalization of mathematics helps to maximize and ideally pump the second stage (Rigorous), and it is on it that most students usually get stuck.
I studied quite well at the university in the IT faculty (Institute of Computing Systems and Programming (Institute 4) at SPB GUAP), and even received the "GUAP Student of the Year - 2017" award. In general, there was a good educational program, but some points can definitely be improved at the GOST standards level. One of these points is too many lectures on theoretical subjects and the lack of seminars on them with an emphasis on covering (building) theory. Example 1 - we had a subject "Abstract Algebra", which I was interested in. But the seminars on it did not correspond to what was given in the lectures - we solved computational problems instead of proving theorems from scratch. Example 2 - we had a subject "Mathematical Analysis", but in the seminars we also solved a large number of computational problems - finding derivatives and integrals. I think this is a relic of the past and GOST needs to be changed. Lectures, as a format of education, need to be completely eliminated. They make very little sense in the modern world. You can always find recordings and watching a lecture live is essentially the same as watching a recording online, only inconvenient and almost always of lower quality than a well-prepared recording. Instead of lectures, you need to do many, many seminars with small groups of students of 5-8 people. The professor in the seminar can give the same material as in the lecture, but derive and prove it simultaneously with the students, and take pauses\give students the opportunity to be part of this process. It will be more expensive for the university, but the difference is unlikely to be noticeable to the management.
It is also necessary to warn you about one misconception, which is quite common both on tekkix and (apparently) among students. There is the notorious Gödel's incompleteness theorem, which states: in any sufficiently powerful formal system, there are true statements that cannot be proven within this system. And I often encountered an incorrect (wrong) interpretation of this theorem. Some people think that this theorem implies the impossibility of creating a single foundation from which everything is derived. But such a foundation exists and has existed for a hundred years - and these are the 9 axioms of ZFC! You can ask ChatGPT, "Which branches of mathematics cannot be formalized in ZFC?" - and it will throw you quite rare cases, half of which (suddenly) are from various deep branches of set theory. If you encounter these rare cases, you can simply add additional axioms to ZFC. For example, the continuum hypothesis (CH) is quite a candidate for addition to ZFC, but it was not added because it is simply not particularly needed by anyone. I have not checked, but I believe that all key theorems and statements about modern neural networks can be derived, and the continuum hypothesis will not be used.
Until 2023, my main goal in studying the theory/foundation of mathematics was to understand the foundation of high-level mathematical disciplines - probability theory and mathematical statistics. Under them lies a rather long mathematical stack. Starting from 2023, I switched my main goal to "understanding the foundation of AI". As it turned out, these goals almost completely coincide. Based on type theory, we build mathematical logic, then based on logic, we build set theory, then we move on to building numerical systems and prove the existence of natural numbers based on the axiom of infinity, then we build integers and rational numbers based on natural numbers. After that, we can build a set of real numbers based on rational numbers and move on to the analysis of real numbers. Next, we move on to measurement theory and build probability theory based on it. Further, independently of all this, linear algebra can be derived from probability theory. When we have probability theory and linear algebra, we can move on to mathematical statistics, and after it - to build specific models of neural networks.
To understand the foundation on which modern machine learning is built, you can refer to the courses Mathematics for Machine Learning Specialization (Coursera) and Mathematics of Machine Learning (MIT). We see that the list includes Real Analysis/Linear Algebra/Probability/Statistics/Multivariate Calculus/PCA. I have the impression that the most important of this list is Real Analysis (in Russian it is often simply called "mathematical analysis" or "math"), and Calculus III (multivariate calculus) and Probability (probability theory) are derived from it. And statistics, or rather its most interesting part, is derived from probability theory.
Thus, the central task in mastering the foundation of machine learning is the formalization of mathematical analysis. This task is not new and was solved back in 1977, when a student (graduate student) used the theorem prover Automath to formalize the textbook "Foundations of Analysis" by Edmund Landau and defended a dissertation on this topic. As it turned out, mathematical analysis is very well formalized. This is a very important subject, for the understanding of which it is necessary to think through strict mathematical logic, and many universities use it to weed out students who have not mastered formal methods of thinking and instead think emotionally and live by animal instincts.
Among Western authors, there are 3 good textbooks on mathematical analysis. The most classic one is Principles of Mathematical Analysis by Walter Rudin, it is most often used in English-speaking technical universities. It is good in terms of formal presentation, depth of elaboration, and challenging exercises. The main drawback for me is that it axiomatically sets the set of real numbers R (11 field axioms and the completeness axiom), instead of deriving everything from set theory. There are advantages to this, as building the entire chain of numerical systems can take a lot of effort and time. For example, in another textbook (Analysis I by Terrence Tao), the author spends the first 100 pages of the book to build numerical systems (N -> Z -> Q -> R) based on Peano's axioms. There is also a book Understanding Analysis by Stephen Abbott, and it is very popular among modern students (judging by the reviews on Amazon). I solved the first chapter in 2022, but I didn't like it because it is too informal and leaves too many gaps/holes in understanding. I would prefer to spend 3-5 times more effort and go through Rudin's or Terrence's book, but get a good result without gaps in understanding.
Собственно, книга Set theory and logic by Robert Stoll от 1963 года тоже строит всю цепочку числовых систем (N -> Z -> Q -> R). Но, как мне кажется, Терренс Тао делает это более подробно и потом плавно перетекает в теоремы анализа, ряды и интегралы. Скорее всего, я пойду именно этим путем, т.к. на основе рядов и интегралов можно потом строить теорию вероятности. Например, в книге A First Look at Rigorous Probability Theory by Jeff Rosenthal, есть раздел "A. Mathematical Background", и автор рекомендует использовать его как измерение "входного порога" (пропускной экзамен) в аксиоматическую теорию вероятности. Если вы чувствуете себя комфортно в тех темах, что там указаны - можно переходить к этой книге. Собственно, там половина - теория множеств, а другая половина - это ряды и свойства вещественных чисел.
Есть 2 способа формализовать множество вещественных чисел (R) - через разрез Дедекина (дается в книге Рудина и Столла) и через последовательность Коши (дается в книге Терренса). Я пока не разобрался в этой теме, но, скорее всего, пойду по второму пути (Cauchy sequences), т.к. это более чистый и современный подход, а также последовательности\ряды более релевантны к фундаменту теории вероятности. Но любой способ подойдет, главное, чтобы на итоговом множестве работали (выводились) аксиомы поля, порядка и полноты.
Что касается линейной алгебры - тут можно ссылаться на учебник Linear Algebra Done Right by Sheldon Axler. Если хотите посмотреть конкретную демку, как главы этой книги формализовать внутри Coq, можете посмотреть плейлист Linear Algebra Done Right in Coq, в котором профессор Квин записал 50 часов видеоуроков. Это может повысить вашу мотивацию и дать конкретный пример. Я планирую повторить тоже самое, но мой фундамент математики будет более чистый (без индуктивных типов), а также полностью выводиться из ZFC.
And if you need a good course on Calculus III (multivariable calculus), I can recommend the course on Educator (23 hours, quite comprehensive and pleasant). I completed it a couple of years ago and learned to take triple integrals on paper along with the author.
Next, we need to find out what mathematical foundation ChatGPT is built on. Here you can refer to the course Neural Networks: Zero to Hero, in which the author builds GPT-2 from scratch. I got the impression that the mathematical foundation of generative neural networks (suddenly) does not differ from ordinary neural networks and has its roots in classical machine learning. But I did not delve deeply into this area, and if I am wrong, please explain this topic in detail in the comments.
It should be noted here that the end result of the work of generative neural networks at the moment is something like a black box and (as far as I understand) is not formalized. I think it's a matter of time. Programming was also once considered more of an art than a science. And then Knuth came and laid a clear mathematical foundation for the analysis of the complexity and correctness of algorithms, reusing the existing mathematical apparatus of algebra/calculus/set theory and graph theory, and also borrowing the Big O notation from Landau. I am sure that the same thing will happen with neural networks. I am 80% sure that some existing branches of mathematics that already exist and are fully compatible with ZFC will be reused. I am 95% sure that even if new branches of mathematics appear, they will be made compatible with ZFC. I am 99% sure that even if a new foundation of mathematics appears, it can be expressed within type theory and formalized within Coq.
Also, there is an interesting book Neural Networks from Scratch (https://nnfs.io/), in which the authors use only Python and its standard libraries to build simple neural networks. I haven't tried it yet, but I plan to try it in the future. For learning, these approaches are the best.
If you are interested in the topic of taking online courses in general, then at my previous job (when I worked at Sravni as a Java developer) I recorded a large meetup on this topic, you can watch the recording here. And now, I work at EDNA as a Java developer.
Announcement of my meetup on online courses
This is Yaroslav, a Java developer from the Core/AF team. A month ago, I conducted a survey on the topic "Who is interested in online courses?" and saw great interest. Aleksey Dolgushev and I did a lot of work in a month and prepared an interesting and comprehensive report. Already this Wednesday (tomorrow) from 12.00 to 13.00 will be the presentation itself [Sravni Tech Meetup], I will conduct it remotely for you (30 minutes of the report itself and 30 minutes answering your questions). In the report, I want to share my experience: in 5 years I have completed (fully) more than 15 online courses; platforms: Coursera, Educator, and TeachIn (MSU). At the meeting we will discuss:
- Why take online courses at all; what are the benefits
- Demotivators that prevent people from taking courses
- About full-fledged online education remotely from top universities in the world
- Where to look, where the right courses live
- How to choose a good course
- Life hacks: how to get free access to paid content, how not to drop the course in the process and other tips
And now let's talk more deeply about type theory. Actually, Rob in his book gives 11 simple type inference rules that are very easy to program and on which everything is built. He argues that you can take any classic math textbook and fully algorithmize it. Any thought process of any mathematician, even the smartest and most complex, can be represented as a chain of N applications of these rules. If you have taken any theory textbook and cannot translate each of its steps into small steps and reduce everything to logic - then your preparation is not deep enough. Any (sufficiently deep) math textbook = definitions + derivation of new results based on previous ones + a small text description that can be discarded.
You can draw a parallel with the Coq documentation, which describes 19 rules for deriving ordinary types and also here 4 rules for deriving inductive types. Coq has greatly expanded the basic rules to make it easier to maintain large formal software verification projects, while remaining compatible with the golden classic of the Calculus of Constructions.
The reader may wonder - why exactly 11 type inference rules? Could there be fewer? Yes, there can be, there is PTS (Pure Type System), which erases the boundary between term and type. Also, there is combinatorial logic, which has only 3 symbols (combinators) S, K, and I. It has been proven that any type inference rules can be reduced to these 3 combinators and combinations of them. If you want to go the extra mile, you can write a combinatorial logic engine in which you build 11 λD type inference rules based on these combinators, and then build everything else on them and do exercises from the book. But in my opinion, this is already overkill, since the 11 λD rules are quite simple to implement and understand, and they are the basis of the Coq and Lean theorem provers, so it makes sense to take exactly the 11 λD rules as a basis.
It should also be noted here that at each stage you can "cut corners" and instead of deriving something, you can simply plug the hole with an axiom. This is very bad for learning and depth of understanding, but it should be borne in mind that this approach exists:
Instead of deriving the rules and concepts of mathematical logic from type theory, you can simply add a dozen or so axioms. For example, for conjunction (A ∧ B) there will be 4 axioms - one postulates the existence of the conjunction itself as a type, another derives (A ∧ B) from A and B, and the other two derive A and B from (A ∧ B). If you want to quickly develop your theorem prover based on first-order logic, you can go this route. But it is better to understand the type inference rules and do everything based on them.
Instead of deriving the Peano axioms (5 pieces) from the ZFC axioms, you can simply postulate them as axioms. For example, Terence Tao does this at the beginning of his book Analysis I, otherwise his book could increase by one and a half times.
Instead of deriving all sorts of concepts like "pair (a, b)", its property and the existence of the Cartesian product from set theory, you can simply accept them as primitive and add them as axioms.
Instead of deriving the entire chain of number systems (N -> Z -> Q -> R), you can immediately move on to the properties of R and postulate the existence of the set R and the axioms on it (field + order + completeness). Many courses in mathematical analysis do just that.
Any too large and thick theorem in probability theory or statistics can be taken on faith and added as an axiom. In fact, many courses and textbooks on statistics do this for most theorems.
Mathematicians can be divided into 2 large groups - algebraists and analysts. Here you can refer to the corn experiment, which showed that representatives of these two directions eat corn differently. It seems to me that most programmers in the industry are algebraists, and most statisticians/data scientists are analysts. Actually, the school subject "Algebra and the beginnings of analysis" introduces the basics of these two directions. When I was in school, I liked about 60% of what we did in school mathematics (the algebraic part), and I didn't like the other 40% (the analytical part). Actually, now I am developing analytical thinking and I hope that my interest in the foundations of mathematics will help me master both of these directions and eat corn the way I want.
I have always been curious about how exactly the transition from the algebraic form (N = A ∪ ∅) to the analytical form (p -> q -> r) occurs. On forums (StackOverflow / Quora), it was written that all mathematics can be reduced to a small set of axioms and any mathematical statement can be traced in the form of a huge tree of logical conclusions (implications), but it was unclear to me how exactly the algebraic form fits into this tree. In chapter 12 "Mathematics in λD: a first attempt," Rob Nederpelt revealed this mechanism and introduced iota-descriptors. It turned out to be very compact and neat, fitting into just 6 lines. He added them as 2 "pseudo-axioms" (primitive definitions), but in essence, they are not axioms and do not make type theory logically stronger (and this has been proven). What they actually do is add "mathematical sugar" for those mathematical objects that (it has been proven) exist and are unique. For example, you can prove once that there exists an empty set and only one, name the theorem empty_set_unique, and then refer to this set through (ι _ (empty_set_unique)): Set. Then, you hide this iota under the term ∅, and use it as it is commonly used in all mathematical texts. If you need the property of the empty set, you can expand the term ∅ back into iota and extract the property from it.
In fact, all classical mathematical texts use iota-descriptors implicitly. Even your school math teacher used it many times on the board when he wrote N and referred to the unique set of natural numbers. Under it hides iota, and under iota - the proof of the existence of this set and its uniqueness.
It is also possible to see how iota-descriptors are defined in the standard Coq library. Essentially, it is the same thing, but complicated by the use of additional definitions and inductive types. For learning and understanding/first acquaintance, this complication is not needed at all and is confusing. This is another reason why it is better to study from a textbook with an emphasis on pure theory, and then move on to specific implementation.
Another interesting and simple example is what is an array? What do you see as a programmer when you think of an array [a, b, c], but without considering the order of the elements? I always saw 3 memory cells (4 bytes each) that store the variables a, b, c one after another. And now, I see something else - I see a logical expression ∃b. ∀x. ((x ∈ b) ⇔ (x = a ∨ x = b ∨ x = c))). And if you take the order into account, it will be a function (a set of pairs) that projects the set {0, 1, 2} onto the set {a, b, c}, i.e. ∃b. ∀p. ((p ∈ b) ⇔ (p = <0, a> ∨ p = <1, b> ∨ p = <2, c> ))). And a pair can also be expressed through a set. In general, everything in IT is perfectly formalized.
Formalized mathematics is sometimes also called mechanically checked mathematics. If you are close to the engineering approach, you can imagine mathematics as a huge factory, where a set of 9 axioms serves as raw material, and 11 type inference rules serve as the assembly standard. Small factories produce proof objects from this raw material, and then roll these proof objects along the conveyor belt to other factories. Maybe I played too much Satisfactory.
It should also be noted here that mathematics (historically) is usually studied from the specific to the general. First, you need to master Calculus, understand its applications, and develop intuition around calculating specific mathematical objects and solving specific problems, and only then move on to Real Analysis. Here you can refer to the failed New Math experiment in the USA in 1970, when they tried to introduce the foundation of mathematics (set theory and symbolic logic) into the school curriculum, and replace them with the tedious memorization of the multiplication table\solving equations and so on. As it turned out, this is a bad idea - first you still need to form some dirty base and spend effort\time on it (and this will surely cause discomfort), and only then move on to something more abstract and pure.
Now let's talk about technical tools that implement type theory within themselves and solve various practical problems. Let's start with Coq (also known as The Rocq Prover). It is a classic in the field of formalizing mathematics and formal verification of software. Coq appeared in 1984 and occupied this niche quite tightly. There is also a newer competitor to Coq - this is Lean. But I did not find enough motivation to take it from the very beginning or switch to it:
Lean is built on the same type theory as Coq, so it has no fundamental advantages.
In the Lean documentation, I did not find a strict formulation of the type inference rules (which Coq has), and this is a bad sign.
Lean is 24 years younger than Coq, which means the community and ecosystem are much smaller, as well as the base of solved problems and applications is much thinner. For example, Coq's reddit has 2500 members, and Lean's reddit has only 390.
A large state research center in France (INRIA) pours a lot of money into Coq, and Lean is funded by a small research department of Microsoft (but I could be wrong here).
Coq has a 6-volume "Software Foundations". For this alone, I could choose Coq
I chose Coq over Lean for roughly the same reasons I once chose Java over C#. But besides Coq and Lean, there are other theorem provers. Isabelle/ZF and Metamath also derive everything from ZFC, but I did not choose them due to their low popularity, as well as their overly custom cores and lack of a strict fundamental theoretical basis.
We have 3 possible levels of applying type theory for formalizing mathematics:
Level 1 - we use type theory only as an engine for mathematical logic, and then we forget about it and work entirely within mathematical logic and derive all mathematical structures from axiomatic set theory. This approach is the most labor-intensive, but it gives the best result for learning and deep understanding. Since my goal is precisely learning and understanding, I adhere only to this approach.
Level 2 - we use type theory not only as an engine, but also transfer some fragments of set theory into it. The result is much more compact and convenient for practical verification tasks, but not very good for learning. For example, instead of deriving the set of natural numbers from the axiom of infinity, we can represent natural numbers as an inductive type, or cleverly introduce them through iota. This approach is used by Rob Nederpelt in his chapter on set theory, and it is also used in the standard library of Coq. I do not like this approach at all, as it breaks down on things like "how to represent a subset?" or "how to represent the set of all subsets (powerset)?" and there you have to use hacks.
Level 3 - we completely move to type theory and use it not only as a foundation for logic, but also as a foundation for mathematical structures. Here we can note the work of our compatriot Vladimir Voevodsky, who developed homotopy type theory and even founded the Coq library for it. But this is a research area, and I do not yet have the motivation to delve into it. It is so not ready that even at the beginning of the textbook on homotopy type theory it is written that the theory is in the process of change and everything can change. Maybe someday I will watch a course of lectures on homotopy theory and try to figure out how exactly it fits with type theory and where it can be applied in my tasks.
If you are interested in specific applications of Coq for solving real-world problems, you can refer to CompCert - a fully formally verified C compiler. During its formalization, researchers found and fixed 100+ critical bugs, and as a result, airplanes fly more reliably. There is also a more recent project - CertiKOS, a fully formally verified operating system that cannot be hacked by logical methods. Its formal verification took 1 million lines of Coq code. Coq is also used in the verification of various things in information security, such as the TLS protocol.
There is also work on the formal verification of neural networks as well, and I am sure that this direction will grow significantly in the near future. People are very afraid of a machine uprising, so they will invest a lot of money to make AI safe and reliable. To give such a guarantee 100% - mathematical methods are needed.
If you are interested in the situation in the theorem prover industry as a whole, everything is very good. You can refer to the list of the 100 most popular theorems and the list of theorem provers in which they are proven. It can be seen that the total coverage is 99 out of 100 theorems - each of them is covered in at least one theorem prover, and Coq covers 79 theorems. Special attention can be paid to the theorem-proof of the irrationality of the square root, which plays the same role as the "teapot" in 3D graphics for testing engines, and all theorem provers prove it. You can also pay attention to the Central Limit Theorem, which is covered only in the Isabelle theorem prover. It seemed to me that it plays a very important role in mathematical statistics and I promised myself that I would not return to the statistics textbook until I formalize this theorem and understand completely how it works from the inside.
You can also mention the QED manifesto project, whose goal is to formalize and computerize all mathematics. So far, the QED utopia has not been achieved, but the Mizar Mathematical Library project has come closest to it. I think in the future, thanks to AI, this project will be revisited and the QED utopia will be achieved. You can read the manifesto itself, it is written in quite understandable language and addresses popular misconceptions about the incompatibility of logic, paradoxes, and so on. It argues that such a project is technically and logically achievable.
I recommend everyone who can program to go through at least the first chapter of the first volume of "Logical Foundations". It does not require special preparation and will take you a couple of weeks. Within this chapter, you will build natural numbers (N) based on inductive types, as well as their basic properties (Peano axioms), and basic operations (addition\multiplication\exponentiation\factorial). You will also get acquainted with the principle of Coq and its basic tactics.
If you are a developer in the industry, you are probably used to writing imperative programs and only occasionally using functional programming. Although some jobs may emphasize functional programming due to the specifics of the business and/or the chosen technology stack. For example, at Edna we use the Reactor project and the reactive approach quite often, and in previous jobs I often used the Stream API. In the case of Java, we have the JVM and the processor's work is imperative by nature, and functional programming is emulated within the imperative computation model (RAM model). But in the theorem prover industry, it's the opposite - the basis is type theory based on lambda calculus, which is completely pure and functional. And the imperative approach is achieved by introducing a tactics language and automation. There are 2 ways to program mathematical theorems - directly through lambdas, as well as through tactics that spin these lambdas under the hood. Any Coq theorem can be represented as a huge tangle of lambdas. The "Show Proof." command prints you the proof object (low-level proof of the theorem). Coq really likes to hide them, and you need to use a small life hack (Defined instead of Qed) to define theorems so that they are not hidden.
What does the proof of De Morgan's law (¬(A ∧ B) ⇒ (¬A ∨ ¬B)) look like at the lowest level
fun (A B : Prop)(H : forall(_ : forall (C : Prop)(_ : forall (_ : A) (_ : B), C), C)(A0 : Prop), A0) =>exc_thrd A(forall (C : Prop)(_ : forall _ : forall (_ : A) (A0 : Prop), A0, C)(_ : forall _ : forall (_ : B) (A0 : Prop), A0, C), C)(exc_thrd B(forall (_ : A) (C : Prop)(_ : forall _ : forall (_ : A) (A0 : Prop), A0, C)(_ : forall _ : forall (_ : B) (A0 : Prop), A0, C),C)(fun (H2 : B) (H3 : A) =>H (fun (C : Prop) (h : forall (_ : A) (_ : B), C) =>h H3 H2)(forall (C : Prop)(_ : forall _ : forall (_ : A) (A0 : Prop), A0,C)(_ : forall _ : forall (_ : B) (A0 : Prop), A0,C), C))(fun (H2 : forall (_ : B) (A0 : Prop), A0) (_ : A)(C : Prop)(_ : forall _ : forall (_ : A) (A0 : Prop), A0, C)(H0 : forall _ : forall (_ : B) (A0 : Prop), A0, C)=> H0 H2))(fun (H2 : forall (_ : A) (A0 : Prop), A0) (C : Prop)(H0 : forall _ : forall (_ : A) (A0 : Prop), A0, C)(_ : forall _ : forall (_ : B) (A0 : Prop), A0, C) =>H0 H2)
exc_thrd is visible - the axiom of the excluded middle, through which the proof goes (since this rule in this form is non-constructive). There are no other axioms here.
Actually, fun is a lambda and is introduced through the abstraction rule (abst). forall is a Π-type, derived through (form). Prop can be replaced with an asterisk.
Printed by executing the command Eval cbv in deMorganNotAnd. In this simple way, for any theorem proved inside Coq, you can get its lambda form by expanding all definitions.
Of particular interest is that all textbooks in the Software Foundations series are read interactively inside the IDE. This is exactly what a mathematics textbook of the future should be - 100% mechanically formalized and verified, the presentation of the material is mixed with exercises, and there is an execution environment and programming language that allows you to experiment\check\go beyond. Actually, here you can refer to Kevin Buzzard's efforts to introduce the Lean theorem prover at Imperial College London into mathematics programs (The Xena Project). I strongly support such things and think that mathematics education will be exactly like this at all levels.
There are two ways to study mathematics - from teacher to student (classical approach), and also with a computer and without a teacher (new approach). Of course, it would be great if good teachers were available for all subjects, and students would enjoy spending time with them. But in practice, there are a lot of problems with this approach. They are not only financial (a good tutor/mentor will be very expensive), but also tied to the place of residence (it is not always possible to find someone available). And it is also very difficult to find someone with whom you enjoy and feel comfortable spending time, someone you like. As a result, alternative directions have to be developed. One such direction is to watch online courses and videos, in which you get the impression that the lecturer is communicating with you, and you solve problems in parallel with him, like with a tutor. Another direction is various interactive environments and compilers/sandboxes that strictly limit your actions and give informative error messages if you do something wrong. In this sense, theorem provers like Coq are the "ideal teacher" of mathematics, which sees 100% of your logical errors and simply will not let you move on if something is done wrong.
I have a hypothesis that during the study of (real) mathematics, something like type theory is formed in a person's head at the level of neurons. I cannot yet confirm my guesses and refer to research in the field of neuroscience, but I believe in this hypothesis and am sure that in the future something similar will be experimentally proven.
Another life hack - if you are a girl and really want to get into IT, you can try living with a man who works as a programmer in an IT company (but not with me) for a couple of years. If you talk about everyday topics every day, you will adopt his way of thinking and absorb basic ideas, even if he does not explicitly teach you. This is super important and can greatly help you later in developing programming skills or a QA/HR profession. But even if you don't master anything, you still have a chance to break into IT with a high salary. I have occasionally met colleagues who know nothing/can't do anything, but think like a knowledgeable/skillful person (mimic a programmer) and are good at passing interviews.
And if you are a man, then wait for the appearance of virtual teachers/mentors based on GirlfriendGPT, they will help you solve the main problem in education - the problem of motivation.
Now let's talk about the topic of "getting into IT". The main reason why ordinary people cannot comfortably get into IT and learn programming is the lack of mathematical training and difficulties in obtaining it. Here is a secret on how to turn an ordinary person into a good programmer: you need to spend a couple of years on school mathematics and bring it up to the level of physics-mathematics schools, and only after that move on to programming languages. Jumping straight into courses or online systems like JavaRush without a solid mathematical foundation is a very bad idea.
If you are interested in where I gathered so much useful information on the topic of fundamental mathematics and connected everything together, I can reveal my sources. I have been actively using English Google for 8 years (almost every day) and communicate with it on various topics. It gives me links to the English Wikipedia, as well as to various sites like MathOverflow, Quora, and Reddit. In 2024, ChatGPT matured as a replacement for Google, so in December I bought a ChatGPT Plus subscription and switched to it as my default search engine in Chrome. I plan to completely abandon Google in 2025 and use only ChatGPT, communicating (or talking) with it in English.
And now let's talk about the list of practical applications of fundamental mathematics. The list is quite large and it is only growing, I get more and more different creative ideas every month. It seems that I have everything scheduled for the next 10 years and all my development and growth in the future (both personal and professional) will involve type theory\set theory\theorem provers.
Application #1: Enter AI/ML and do it royally. From my experience with computer science, I know that the deeper the theoretical preparation, the better. This is not only the entry threshold, but also a foundation for development, a wider choice of companies, the possibility of migration within the company, flexibility in development and resistance to downsizing. Somewhere in 2026-2027, I will be ready and immediately take some cool courses from Coursera or MIT OpenCourseWare on AI. It is not at all necessary to fully formalize the entire foundation for AI/ML. I think that a deep understanding and formalization of some key theorems in analysis and probability theory will be more than enough.
Application #2: Algorithms and data structures, their analysis and formalization. Actually, I have already worked quite deeply in this area and completed 2/4 courses from the specialization on Coursera in algorithm design and analysis from Stanford University in 2022. My main goal is not only to comfortably pass algorithmic interviews and have a strong position in the market, but also to be able to take on cooler and more interesting tasks. I don't know exactly how I will progress further, but I do know that I want to formalize the Turing machine within ZFC and learn how to run it there, as well as understand how the RAM model (mathematical assembler) is compiled into the Turing machine. If this is done, one can achieve a 100% understanding of the very concept of the algorithm and, as a result, get a big bonus in solving algorithmic problems. It would be ideal if I could solve algorithmic problems on LeetCode simultaneously in two languages - a mathematical model and proof of correctness\complexity in Coq, and a fast implementation of the algorithm in Java.
It should also be noted that among programmers in Russia there are a lot of weak IT specialists with very poor mathematical training, who solve rather routine and uninteresting tasks in projects with poor quality code base, and also do not want to learn something new and invest in development. Such a development path was not promising before, and now (taking into account changes in the world of AI) it seems completely disastrous and I strongly recommend that you do not listen to the opinions of such acquaintances if you have them.
Application #3: Software Formalization. As I mentioned earlier, Coq is actively used in the industry to prove the correctness of programs and any IT systems in general. I initially thought that this was too narrow a direction and generally not very useful for a Java developer's career. Now I don't think so. In my work, I regularly encounter situations that are critically important for the business and that directly call for formalization. Formalization will not only provide a more clear/argued answer to the business (relevant for the tech lead), but also prevent incidents in production (and allow for rest instead of fixing them). For example, microservice interaction and some architectural patterns directly call for formalization. Companies spend a lot of money and mistakes are very expensive. It is better to convince the business to put this money in the Java developer's pocket.
Actually, a year and a half ago I solved the first 6 chapters 100% in the Logical Foundations textbook, but got stuck on the chapter "Inductively Defined Propositions", as it (apparently) is of increased complexity. At that time, I did not have such a deep theoretical background as I do now. Now I can go back and finish the first volume. I will do it in the next couple of years if there are no more interesting priorities.
Application #4: Database Formalization. Databases are used by all IT specialists (even managers), and the obvious question arises - how to formalize relational databases? In 2021, I came across a very cool book Applied Mathematics for Database Professionals by Lex deHaan, in which the authors very clearly formalize modern databases and SQL in terms of mathematical logic and set theory. This book was a big revelation for me and I quickly and comfortably solved the first 8 chapters and exercises on paper. It not only covers simple CRUD operations, but also more complex topics such as database structure, its constraints, and transactions.
Actually, this is very useful for a deeper understanding of the logical essence of the database (what is important in the database and what is secondary), it helps not to drown in the details of the implementation of a specific database, but to focus on the key points and design the database more competently.
Example of Select and its formal form in the language of set theory
select distinct e.JOB from EMP e where e.MSAL > 4800 or e.SGRADE >= 6
Application #5: Development in management. I have the impression that good managers (especially top managers) are very educated people and they use mathematics to the maximum in their work. We are talking not only about simple statistical data analysis, but also about the construction and testing of hypotheses, the use of Data Science tools, as well as the application of various interesting things such as Game Theory/Optimization Theory/Linear Programming for making major strategic decisions. Actually, you can try to develop in this direction and earn a lot of money, which will pay off the costs of fundamental mathematics many times over. You can also try to combine management theory, PMP certification, and generative neural networks to create something interesting and creative.
Here I want to note that among my acquaintances I have met many examples of bad managers - who go into management due to professional degradation and laziness, receive a salary much lower than a good programmer, and also use very primitive tools and personal (sometimes emotional) experience in making decisions. I do not consider such a development path in principle, and by the word "manager" I mean exactly the mathematical manager that I described in the paragraph above.
Application #6: Develop your own 3D engine and your own 3D game. I started programming at the age of 13 with developing my own games and 2D engines for them in 2007. Since then, I have dreamed of trying to develop my own 3D game - as a hobby and for fun. I still have to deeply master linear algebra for ML, and as a bonus and motivator, I can make my own 3D engine from scratch with a full understanding of the foundation.
Application #7: Deeply understand evidence-based medicine. I have the impression that the best part of medicine is the one based on mathematical statistics. And the medicine of the future will be exactly like this, it needs to be completely reduced to statistics and probability theory. I am very interested in this direction and for the sake of it alone I could spend a couple of years studying. Mathematics can not only help intuitively understand complex research and articles in medicine, but also try various interesting projects, such as Hummod (the most complete mathematical model of human physiology ever created).
Application #8: Deeply understand how the real world works at a low level. I have had a dream since school - to write a program that derives the periodic table from the laws of quantum physics and predicts chemical reactions, as well as lays the foundation of chemistry. But at that time, I lacked both the algorithms and the deep understanding of quantum physics and its mathematical basis. Actually, in the near future, I can try to master and formalize differential equations and then make something like a quantum world simulator. But when I get around to it - I don't know. Now I am 31 years old, and there is so much to learn and try, there are many other priorities. Maybe when I am 50+, I will return to this issue.
Application #9: Write an uber-dissertation on the mathematical foundation of ChatGPT. Actually, I already studied at ITMO graduate school (2017 - 2020) at the Department of Computer Science and Applied Mathematics (CSAM), but at that time I did not have a real research project, so I passed the academic minimum and left. As I accumulate the mathematical foundation, I understand that it is ideal for writing a dissertation. It will be cool if I really manage to go all the way from type theory to the theory of generative neural networks and get a PhD in this field. But when I will have free time for this - I do not know. I think that the machine uprising will start sooner than I will have time to defend my dissertation...
My main goal in writing this article is to get as much feedback and comments as possible and to adjust\complement\expand my plans for the future. I will be glad to hear your comments, recommendations, advice, and criticism. The more you write, the better. You can write in the comments, by email ([email protected]) or in Telegram by personal message.




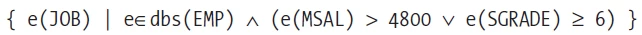







Write comment