- Security
- A
What determines the security of a quantum network? Part 1
Quantum key distribution [1] is one of the most rapidly developing areas in modern science. The most important advantage of QKD is the security of personal data transmission with quantum-distributed keys, based on the laws of quantum physics, rather than mathematical algorithms. The latter can be hacked, but it is impossible to deceive the fundamental laws of physics.
Authors — Andrey Gaydash, Georgy Miroshnichenko, Anton Kozubov
LLC "SMARTS-Kvantelecom"
Quantum key distribution (QKD) [1] is one of the most rapidly developing areas in modern science. The most important advantage of QKD is the security of personal data transmission with quantum-distributed keys, based on the laws of quantum physics, rather than on mathematical algorithms. The latter can be hacked, but it is impossible to deceive the fundamental laws of physics.
Work on the development of QKD technology can be considered as a basis in the processes of secure data transmission over the global network. Only a few network topology options have been proposed and analyzed until recently, along with the main transport schemes and their security assessments [11-21]. However, the existing limitation in the distance between two neighboring nodes pushes for the development of large-scale quantum networks that could cover large areas or become backbone networks connecting cities and countries.
To date, there are two types of networks: with a trusted and untrusted node. The latter is based on the operation of a quantum repeater, which requires quantum memory. At the moment, neither the quantum repeater nor the quantum memory can work to their full potential due to the underdevelopment of modern technologies. Nevertheless, extensive theoretical research on this topic can be found [26-28].
In practice, there are also cases when only one untrusted node may be available, which uses device-independent QKD (MDI) protocols [29-37] (however, it should be noted that this is not the motivation for MDI). In [38], as an alternative to the single-photon approach, the first implementation of the TF QKD scheme with a coherent state was proposed, which made it possible to exceed the known key generation rate limit without repeaters, namely the lossy channel [39] (also known as the "Pirandola-Laurenza-Ottaviani-Banchi bound") [39,40]. Also in [41-45], several new approaches to the implementation of the TF QKD protocol were proposed - a multi-client version of TF-like QKD. However, despite this, the applications of multi-client MDI or TF QKD systems (similar to the star network topology with untrusted nodes in the center) are combined into one large network by a trusted node, as shown in Fig. 1. Therefore, in addition to quantum repeaters, the option of existing in the paradigm of trusted nodes seems inevitable. That is why it is necessary to consider the configuration of trusted nodes and connections between them in order to assess how the probabilistic properties of each node are transferred to the level of the entire network; of particular interest are the security properties of networks and the key transmission protocols used.
In this article, we provide an assessment of how the introduction of new connections into widely used sequential connections (or increasing the density of connections between trusted nodes of the global quantum network in the future) affects the security of quantum networks. In [11,12], a limited number of compromised nodes is considered; in turn, our model can work with any section of compromised nodes. Our network section configuration (it is implied that we can consider the selected end-to-end path within a wider network) and eavesdropping model are similar to those presented in [13]. However, in our approach, we do not track the presence of an eavesdropper in the nodes by excluding the repeater. One of the goals of the approach is to assess the average probability of successful key transmission, taking into account any possible configuration of compromised nodes and intercepted QKD links. Thus, in this article, we demonstrate the appropriate key transmission technique and a general method for assessing the probability of its successful implementation.
Next, we describe in detail the topology of the considered network section and the key transmission protocol.
CONFIGURATION AND KEY TRANSMISSION PROTOCOL
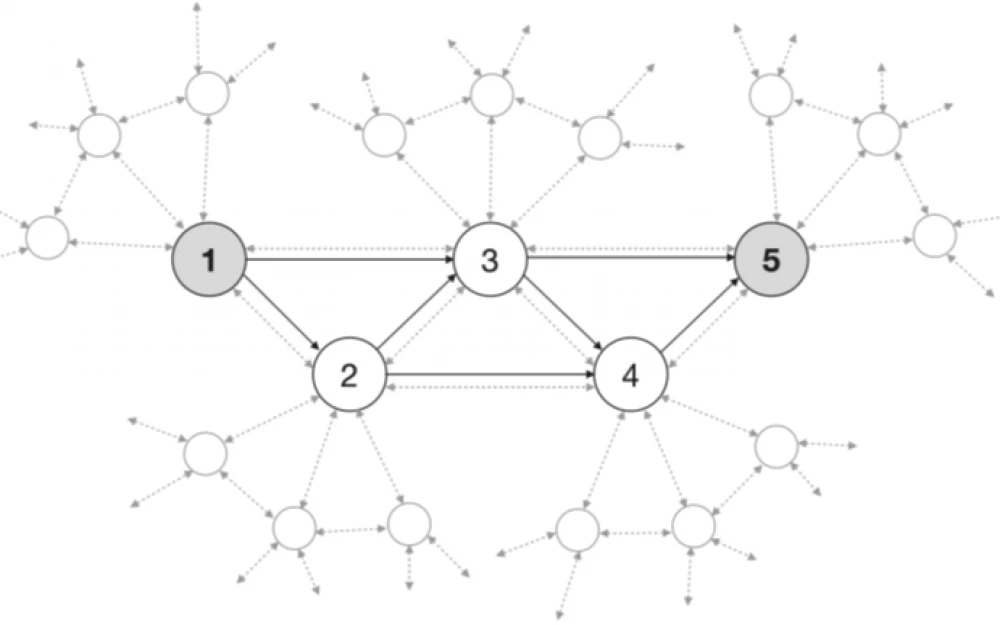
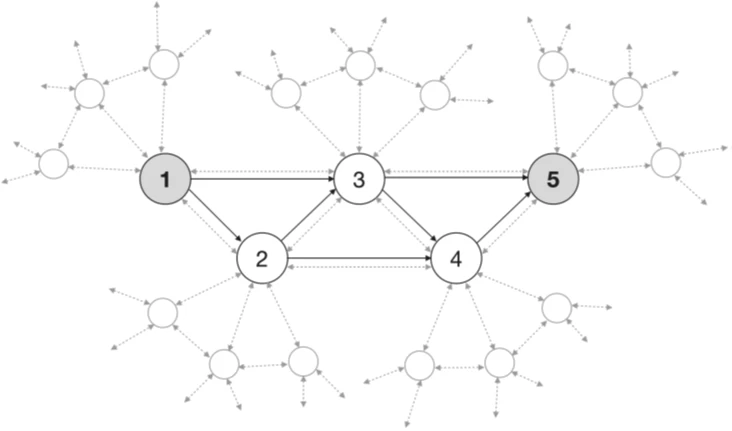
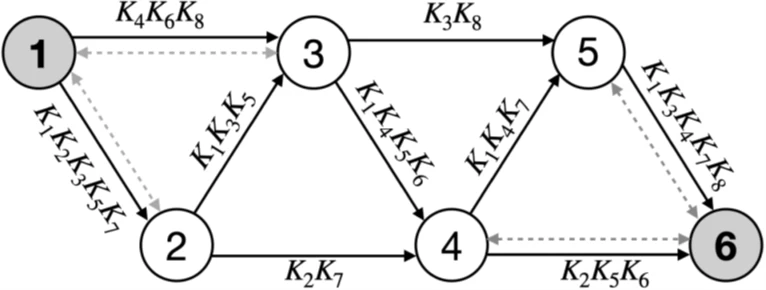
In the second part of this article, we consider a section of the quantum network that connects two users within itself (see Fig.1). Let's pay attention to the part of the network containing N nodes, at least sequentially connected to each other and having additional connections through one, two, and up to s−1 nodes (see Fig.2); the total number of connections requiring QKD links is N − c+1.
Circles are trusted nodes, dashed gray arrows are QKD connections between them (it should be noted that there may be untrusted nodes between them, which are not shown in Figure 1, but are shown in Figure 3), black solid arrows are one-way key movements through any open classical channel. Key movements occur between dark gray nodes for a specific session.
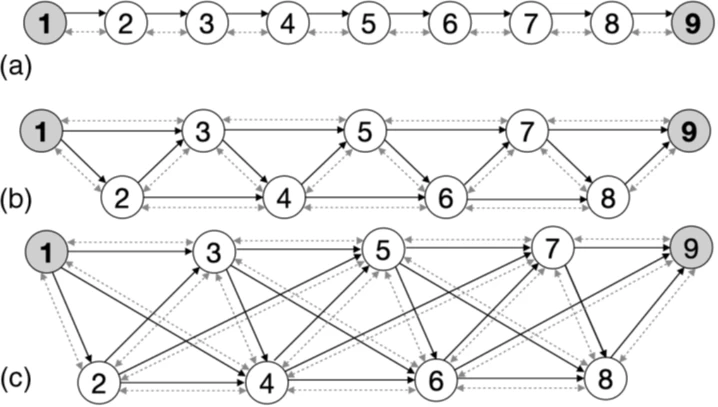
(key transmission session between two gray nodes) with different numbers of additional connections, i.e., connection density. Increasing connections can be seen as increasing the density of nodes and connections in the global quantum network. Circles are trusted nodes, dashed gray arrows are QKD connections between them, and solid black arrows are one-way key transmissions by any OCC. The option with N=9 is considered as an example. (a) Typical sequential connection, c=1. (b) Sequential connection and additional connectionthrough one node, c=2. (c) Sequential connection and additional connection through one and two nodes, c=3.
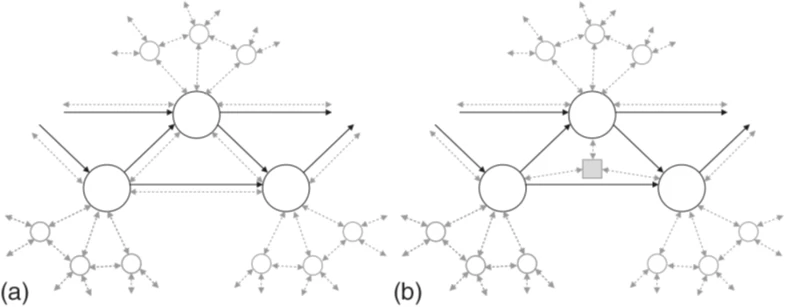
In the figures, QKD connections are indicated by gray bidirectional arrows (without specifying their type, see Fig. 3 as an example); and key transmission over any open classical channel (OCC) is indicated by solid black one-way arrows. Keys are distributed quantumly between each pair of connected nodes. We assume that the QKD protocol used is εkcd-secure, for example, [47]. Classical data encrypted with quantum-distributed keys is transmitted in one direction (at least for the current session). The latter can be explicitly described by the adjacency matrix A, which is a matrix with a unit in the k-diagonal for 1≤k≤c and 0 elsewhere. This configuration describes one-way connections between neighboring nodes and up to c−1 nodes. This simple network configuration implies fairly simple analysis and has useful properties. We also believe that the properties of more complex adjacency matrix configurations can be investigated using perturbation theory or other methods. However, there is a high probability that individual sections in networks with dense node distribution can be described by the adjacency matrix A with symmetric properties, as noted earlier.
Circles — trusted nodes, square — untrusted node, gray dashed arrows — QKD connections between them, and black solid arrows — one-way key transmission over any open classical channel. The considered approach does not distinguish between the two indicated options (a) and (b); in any case, the only limitation is that trusted nodes must equally use the key security parameter εqkd. Gray dashed lines indicate QKD connection between trusted nodes without specifying their type in the other figures in the article.
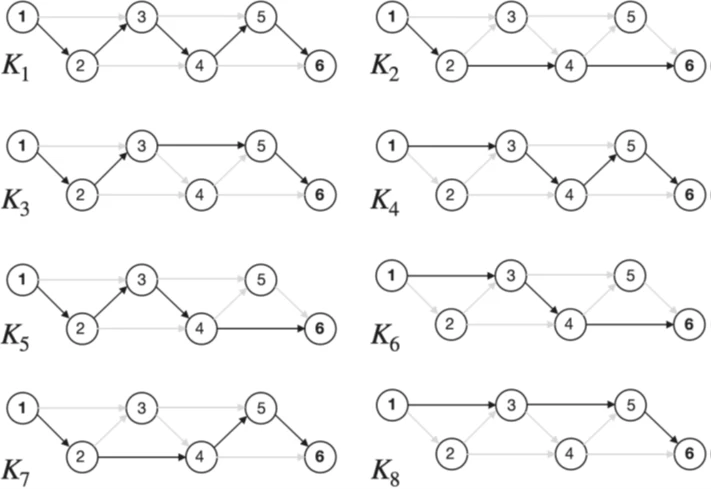
The total number of key transmission routes between users during a specific session is calculated as Φ(c) N, where N is the Fibonacci number (see Fig. 4). Thus, these properties can be applied to create a key transmission protocol similar to [13,15]. Each path is intended for transmitting one of the keys Ki, where 1≤i ≤ F(c) (see Fig. 4 and 5). Quantum-distributed keys are used to transmit several Ki in the form of encrypted messages transmitted over communication channels between nodes. The final key is K = ⊕i Ki, where ⊕ is the bitwise XOR. This key transmission method ensures that one compromised node does not reveal the transmitted key to the attacker (c > 1).
Visualization of all possible key transmission routes, distributed between Ki to sections of the quantum network with N=6 and c=2. Routes represented by black and gray solid lines indicate unused (for certain keys) connections. The total number of routes is F6 (2) = 8, i.e., the sixth Fibonacci number.
Authentication protocols with a failure probability of $$\varepsilon_{\text{auth}}$$ are used before each QKD session to ensure the security of the node. A set of predefined keys is used for such verification, some of which are replenished from the set of quantum-distributed keys. It should be noted that the authentication problem can be solved separately from the QKD problems and then considered according to the composition principle [48]; therefore, we can hope for the presence of at least some security parameter $$\varepsilon_{\text{QKD}}$$ of the QKD protocol and not consider it in detail. The described key transfer protocol will perform its task if there is at least one route passing from the beginning to the very end through an authorized trusted node.








Write comment