- AI
- A
Physics-based и data-driven моделирование
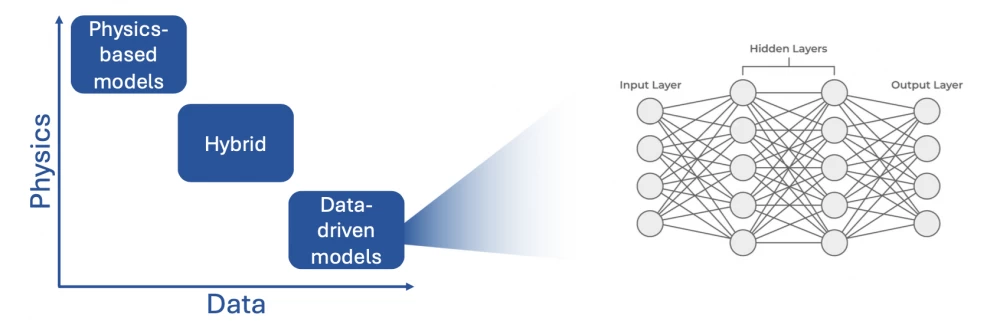
In this post, we will discuss the differences between two modeling approaches, namely, how physics-based models differ from data-driven models. In fact, there is something in between these two concepts that is becoming more relevant in solving scientific problems. But more on that later.
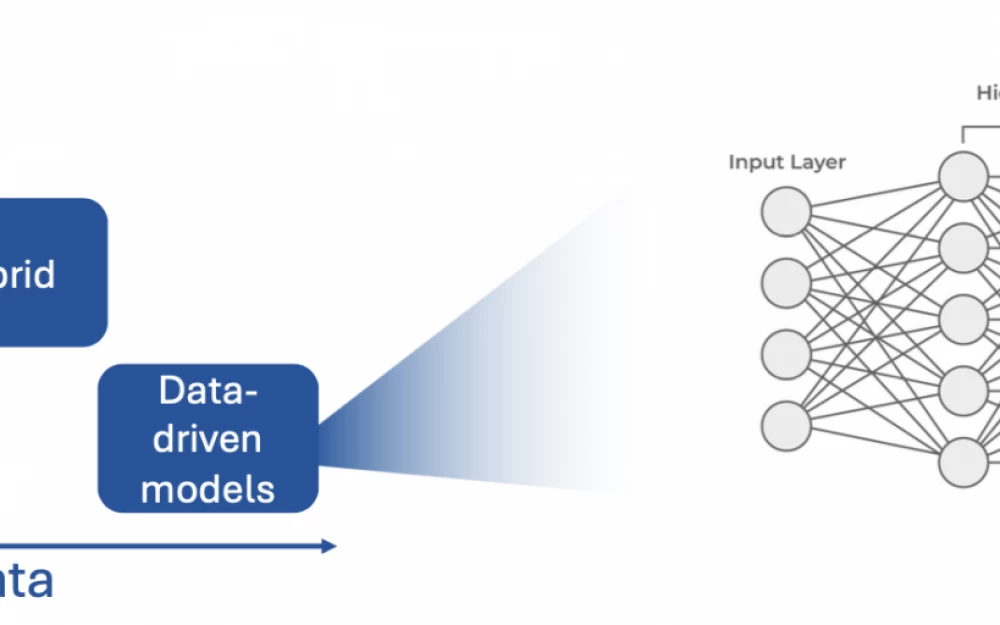
Data-driven models
So, let's start with data-driven models. Such models are found almost everywhere. Any machine learning task, whether it is regression (e.g., predicting product prices), classification (determining a disease marker based on patient test data), recommendation (determining the most suitable video in your feed), segmentation (identifying objects in photos or videos), etc. There are many machine learning tasks, but they all require one thing - data.
In this class of models, it is necessary to collect an appropriate dataset, process it (e.g., remove various anomalies or transform variables), determine the type of task, choose a model for this type of task, and feed the data into the model. And finally, train the model by optimally adjusting the weights.
Data-driven models are essentially statistical models that best approximate an unknown dependency. In many tasks, the relationships between independent variables and the resulting feature or features are unknown. They are either difficult to describe, or we do not have a clear formula for obtaining the answer. This is where such statistical models come to the rescue.
Physics-based models
Physics-based models are models that rely on the laws of physics. Such models are usually written in the form of mathematical equations and have a fairly strict description of variables and relationships between them. In fact, any physical theory consists of a large number of models to describe various phenomena.
Consider a simple example — the oscillation of a pendulum. To describe the position of the pendulum, it is sufficient to use one generalized coordinate, namely the angle of deviation from the vertical
Figure 2 demonstrates a physics-based model — Maxwell's equations, which describe the electromagnetic field. The entire model is formulated using a system of four differential equations in vector form.
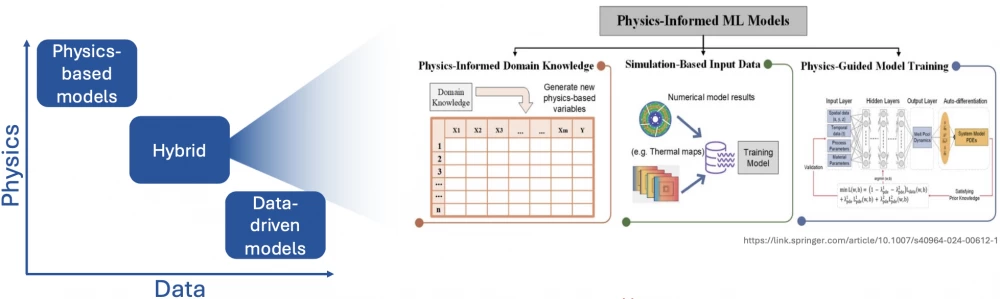
Finally, Figure 3 shows various types of hybrid models. Physics can be used as a source of additional variables, either to obtain data from simulation or as auxiliary elements of the neural network architecture.
The advantages and disadvantages of all approaches are presented in the table.
Advantages | Disadvantages | |
Data-driven | 1. High accuracy Read also:
2. Scalability and flexibility 3. Automation 4. Discovery of previously unknown patterns | 1. Dependence on data quality 2. Overfitting or underfitting 3. Low interpretability 4. Low domain understanding 5. Resource-intensive |
Physics-based | 1. High interpretability 2. High predictive power 3. Generalizability 4. Controllability of parameters | 1. May involve complex mathematical models without analytical solutions 2. Often involves assumptions and simplifications 3. Unstable to new unexplored patterns 4. Sensitivity to initial conditions |
Hybrid | 1. High accuracy (model relies on known physical laws plus reduces error by fitting the model to data) Read also:
2. Scalability and flexibility 3. Medium interpretability (compared to the two previous approaches) | 1. Balance problem between interpretability and quality 2. Resource-intensive 3. Complexity in integration and training |
The purpose of the post was to give a brief overview of the three modeling methods. Next, I plan to elaborate on useful topics from hybrid AI.












Write comment