When AI can optimize...

Hello everyone!

My name is Dmitry and at my last job I was a data consultant and product owner, but now I am more suited to the role of an enthusiast-researcher.

About AI

The next wave of artificial intelligence development has affected almost everyone. Of course, I also discovered in myself a kind of AI madness gene. More correctly, I have always been a carrier of this gene, but I have been preparing for a long time and carefully to meet its manifestation fully armed. And since I was preparing and anticipating, it means I have something to tell. Something different and special, rather than just amazement at how an electric machine writes SQL queries, simultaneously hallucinating all sorts of funny nonsense.

It is known that the toolbox of a modern programmer has a lot of different things: a convenient development environment, a version control system, various CI/CD and containers, high-level programming languages like R and Python, ready-made packages/frameworks, markdown documentation, search engines and stack overflow. It is interesting, what place in this list by priority are AI assistants? I do not exclude that somewhere at one of the last, but the realization of this truth does not change the business expectations from AI as a kind of technological mission capable of turning the world upside down and providing an unprecedented breakthrough in the productivity of white-collar workers. Perhaps, by the way, it will be so.

Let's leave corporate visionaries alone for a while and remind ourselves that the main technological AI breakthroughs of recent times have occurred in the field of computer vision, hearing, and later came generative neural networks capable of creating new content and in some way imitating the thought process wrapped in a chatbot. At this stage, I personally have a question, how capable are modern neural system architectures of "thinking" and making decisions under given optimality conditions? Are neural networks, being a universal approximator, capable of approximating ideal or nearly ideal management decisions? Of course, we are not talking about a wide range of management decisions, but about operational and tactical optimization tasks. Such tasks are usually accompanied by a large context that barely fits into the human skull. Indeed, it is difficult to imagine a person keeping hundreds of units of resources (equipment), their current states (location), and then making an optimal decision about assigning such a resource to the next job. Optimization models come to the rescue, capable of finding an optimal or nearly optimal solution. In addition, clever leather bags are capable of thinking at a different level of abstraction using heuristics. Indeed, it is not necessary to keep the whole picture in mind, but you can establish a policy or a simple rule for managing a resource, for example, to perform the work that is closer/simpler, and such a policy will work almost always or very often. One can recall the traveling salesman problem, where the seller must visit all the cities and would like to do so by the shortest possible route. The simplest solution to such a problem would be to visit the nearest city. It will not be perfect, but definitely better than a random route.

Okay, heuristics are not perfect and subjective, but there are exact algorithms for solving such a problem. Everything is extremely simple at first glance: we take a solver and go ahead to the optimal solution. The simplest solvers can be found in Excel and therefore their wide availability is implied. However, if you look at the algorithms that solve the traveling salesman problem, we begin to feel like we are peering into a black hole of the knowledge of past generations, where the light of our own mind is quickly lost. It turns out that the solver solves this problem not by a frontal attack, but rather by an additional heuristic in the MTZ formulation, which limits the formation of meaningless sub-routes. Moreover, when reaching any value of 20-30-100 cities, the solvers begin to rapidly die (hello NP-hard problems). But the difficulties do not end there. Suppose we spent a couple of hours or even a day to calculate the optimal route, but suddenly some city was closed for quarantine or the road was blocked. The route will have to be completely recalculated and there is nothing you can do about it. Stochastic (inaccurate) methods can help solve the problem, but heuristics are still needed, time is needed to calculate each time again and again, again and again.

Note how the described situation differs from human heuristics, which work always or almost always, and which do not require recalculation. Hence the question - is AI capable of replacing a person in the search for such heuristics? Moreover, due to the fact that such a network has virtually unlimited memory storage resources compared to the human skull, it could have many heuristics in its arsenal with the ability to switch in a timely manner depending on the current context. This formulation already sounds much more interesting than selling sweetened water the task of writing an advertising slogan by a chat bot.

The topic is certainly not simple. Every time of the year I jump with a cavalry rush on the next neural network architecture, I end up encountering existential thoughts with the search for an assembly point in some other more understandable area to escape from the state of despair associated with overloading my cerebellum. Probably, such extraordinary things should be painful, otherwise they would have been solved long ago.
So, it's time to stop graphomania and roll out some code to start analyzing this topic in detail, if it is possible at all.

The code will be written in R. In fact, this should not greatly interfere with Pythonists or lovers of other languages to understand the main ideas, since the language constructs for algorithms are very similar, but have tactical differences in syntax.

Basic MIP Solution

Let's consider the basic traveling salesman problem, known as TSP (Travelling Salesman Problem), and find the optimal route for a set of 16 cities with random coordinates in the range from 0 to 100. Let the starting point No. 1 have coordinates x=0, y=0.

library(ggplot2)

# Forming the traveling salesman problem for 16 cities
n_cities <- 16

set.seed(2021)
cities <- data.frame(x=0, y= 0) |> # the first point is always at the origin
  rbind(data.frame(x = runif(n_cities-1, max = 100), 
                   y = runif(n_cities-1, max = 100))) 

# Visual representation of the problem
p0 <- transform(cities, n=seq_len(n_cities)) |>
  ggplot(aes(x, y)) + 
  geom_point() + 
  geom_point(data = data.frame(n=1, x=0, y=0), shape = 21, size = 5, col = "firebrick") +
  geom_text(aes(label = n), nudge_x = 3, nudge_y = 3) 

p0 + labs(title = "Travelling Salesman Problem for 16 cities")

The exact solution to the problem can be obtained by formulating the problem as an MIP (Mixed Integer Problem) and using a package that allows modeling such problems at the level of relatively simple rules. In this case, the ompr package will be used. There are several approaches to modeling the problem, but in my subjective opinion, the most common is the formulation in the form of the previously mentioned MTZ (Miller–Tucker–Zemlin). The optimization solution code might look like this:

library(ompr) # package for MIP optimization
library(ompr.roi) # package for solver integration
library(ROI.plugin.glpk) # GLPK solver

# Distance matrix for cities
dist_mtrx <- as.matrix(dist(cities))

mdl_MIP <- MIPModel() |>
  # variable that takes the value 1 if the traveling salesman goes from city i to city j
  add_variable(x[i, j], i = 1:n_cities, j = 1:n_cities, type = "integer", lb = 0, ub = 1) |>
  # auxiliary variable for the MTZ formulation of the traveling salesman problem
  # add_variable(u[i], i = 1:n_cities, lb = 1, ub = n_cities) |> 
  # objective function to minimize the route 
  set_objective(sum_expr(dist_mtrx[i, j] * x[i, j], i = 1:n_cities, j = 1:n_cities), "min") |>
  # indication of the impossibility of moving from a city to the same city 
  set_bounds(x[i, i], ub = 0, i = 1:n_cities) |>
  # constraint ensuring that each city will be left exactly once
  add_constraint(sum_expr(x[i, j], j = 1:n_cities) == 1, i = 1:n_cities) |>
  # constraint ensuring that each city will be visited exactly once
  add_constraint(sum_expr(x[i, j], i = 1:n_cities) == 1, j = 1:n_cities) # |>
  # exclusion of subtours
  # add_constraint(u[i] >= 2, i = 2:n_cities) #|> 
  # add_constraint(u[i] - u[j] + 1 <= (n_cities - 1) * (1 - x[i, j]), i = 2:n_cities, j = 2:n_cities)

# mdl_MIP

system.time(res_MIP <- solve_model(mdl_MIP, with_ROI(solver = "glpk", verbose = FALSE)))

##    user  system elapsed 
##   0.078   0.002   0.082

res_MIP

## Status: success
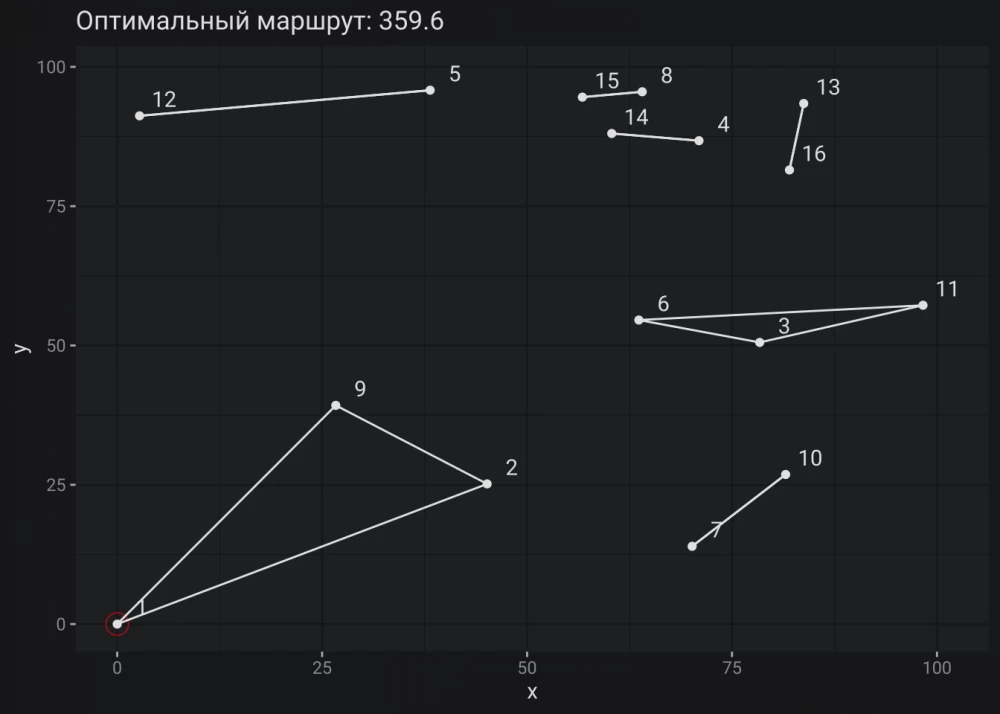
## Objective value: 359.6007

The first part of the model is quite understandable:

• There is a certain boolean variable

  

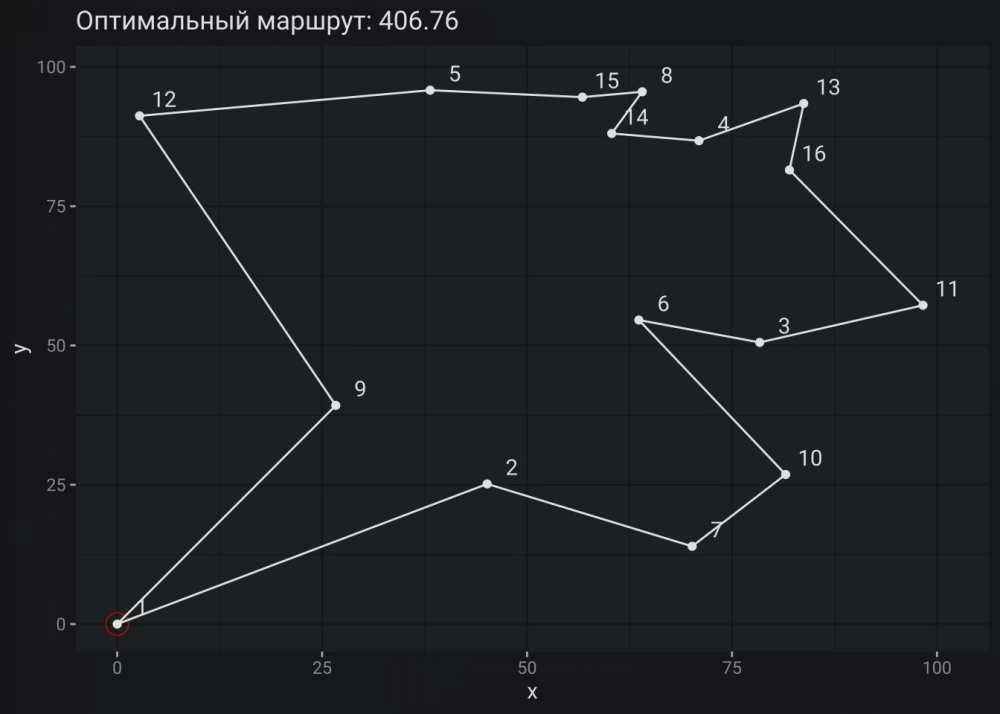
  The graph clearly shows that all the above requirements are met, but there is no single route through all the cities. It's as if our traveling salesman has a teleportation spell. Obviously, this is not what we would like to get.

  Okay, the problem of subtours is now clear and the question arises how to solve it using the auxiliary variable

  

  The optimal route is built. If anyone has doubts about this, you can try to build your own version.

  Afterword

It can be noted that the content of the first part of the note contrasts with the second. The long motivational introduction about AI collapses to an algorithm that will soon be a hundred years old. This is done to bridge several disparate areas that solve a similar problem. Without an exercise with classical methods, it will be difficult to explain all the advantages and disadvantages of using advanced neural network architectures with the use of attention mechanisms and transformers.

In addition, it was simply desired to fill in the gaps in the description of some algorithms. All the descriptions I found, alas, did not satisfy because essential details for understanding were missed. Therefore, I will continue to get acquainted with the old algorithms, which are computationally more interesting than MIP, but do not guarantee an optimal result.

Original note