Sonar from Dictaphone

Problem Statement

Record a *.WAV file during the action of a point sound source generating LFM signal pulses.

Calculate the correlation and estimate the distance to objects around.

Main Idea

I tried to periodically emit LFM pulses and continuously calculate the correlation. Measure the time between TOF peaks and convert it to distance. Just like in real radars.

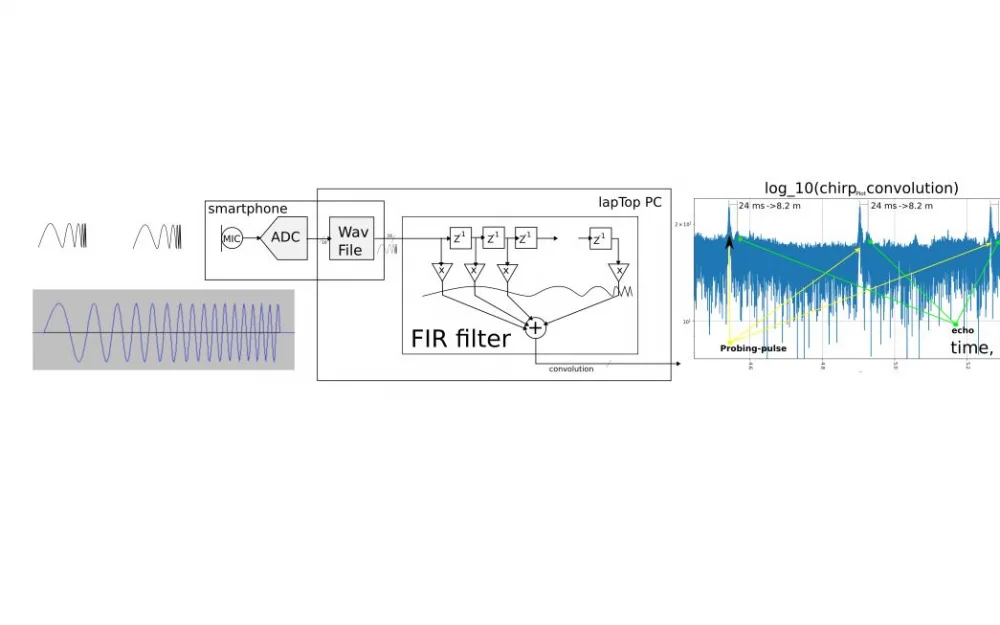
Implementation

As it is known, the speed of sound is 331 meters/s. If you multiply the speed of sound by TOF and divide by two, you get the distance to the object.

For a sufficient number of measurements, it is necessary to emit a series of chirp pulses. In this wav file, the probing LFM signals follow with a period of 0.362 s.

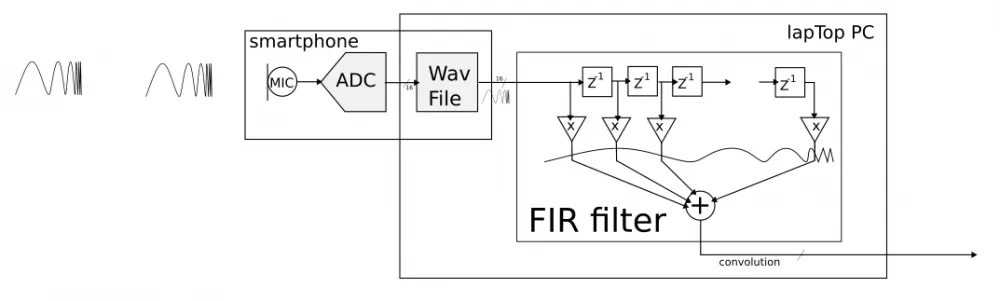
I took two mobile phones and went outside. I turned on the first smartphone to play the *.wav file with the sequence of probing LFM signals, and placed the second smartphone nearby and turned on the voice recorder to record the *.wav file at a sampling rate of 44100 Hz.

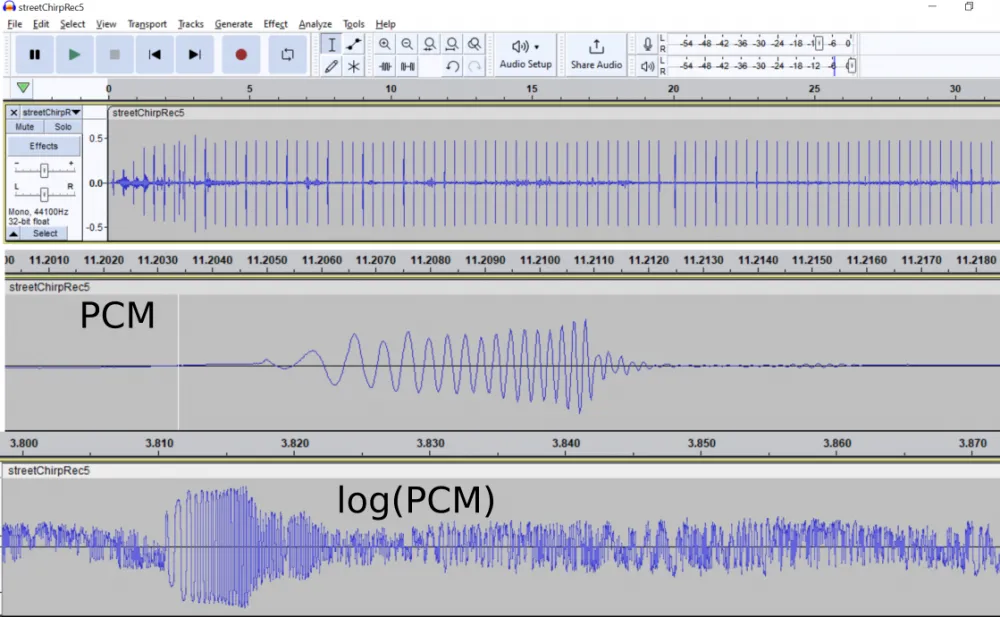
This is the resulting recording file.

Then I took the recording file and fed it into my console utility, which performs the convolution of the recorded file and the same probing LFM signal.

I performed the convolution with an FIR filter whose coefficients are the values of the LFM signal samples.

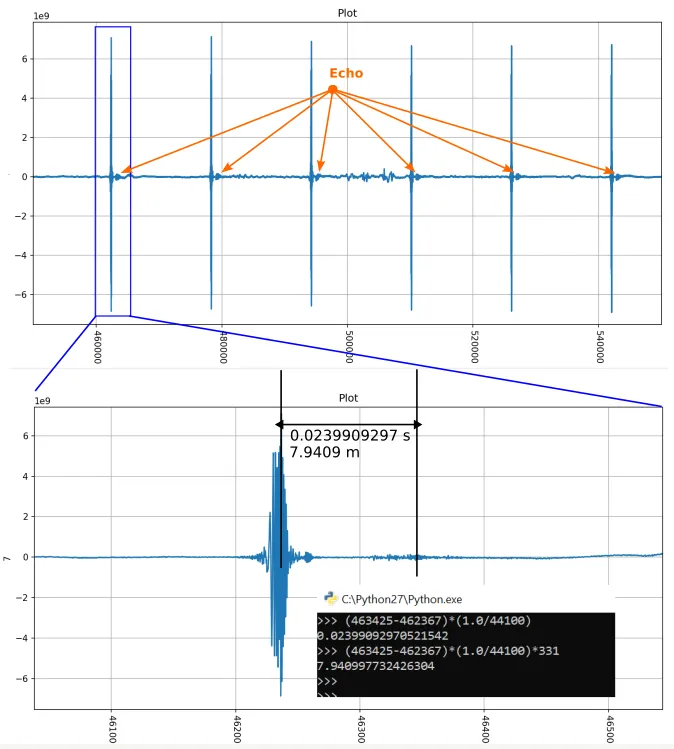
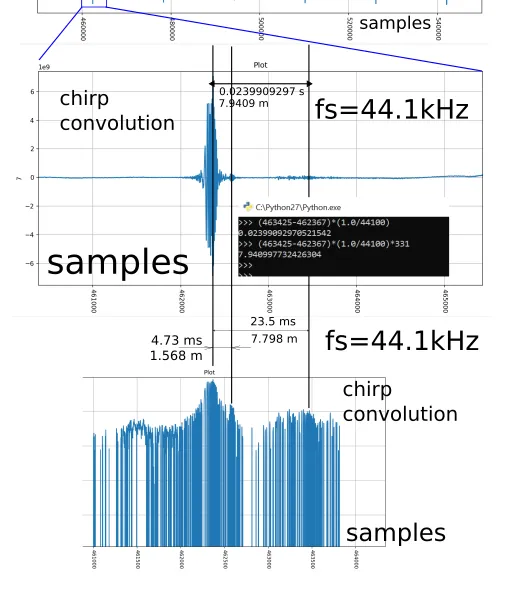
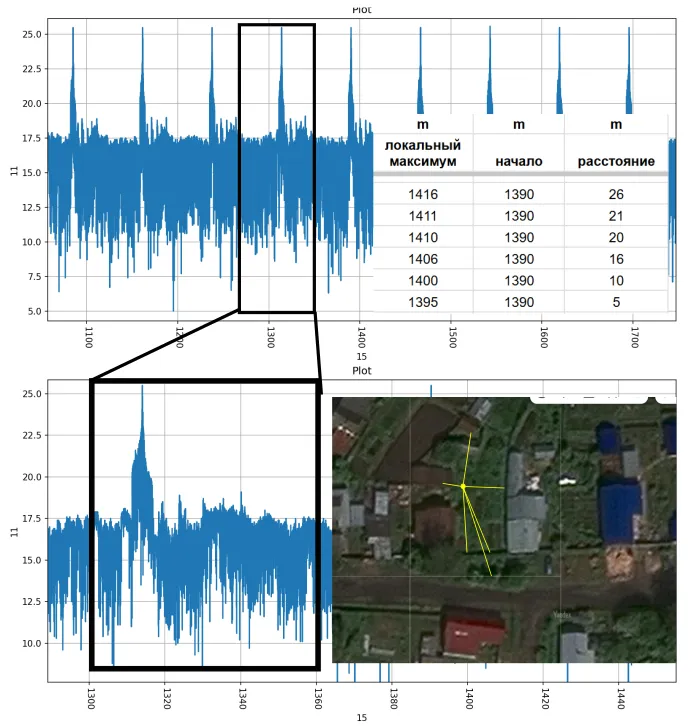
This is the resulting convolution. Here you can see that after 23ms there is a stable echo. Dividing the TOF 23ms by two and multiplying by the speed of sound 331 m/s gives 4 meters to some target.

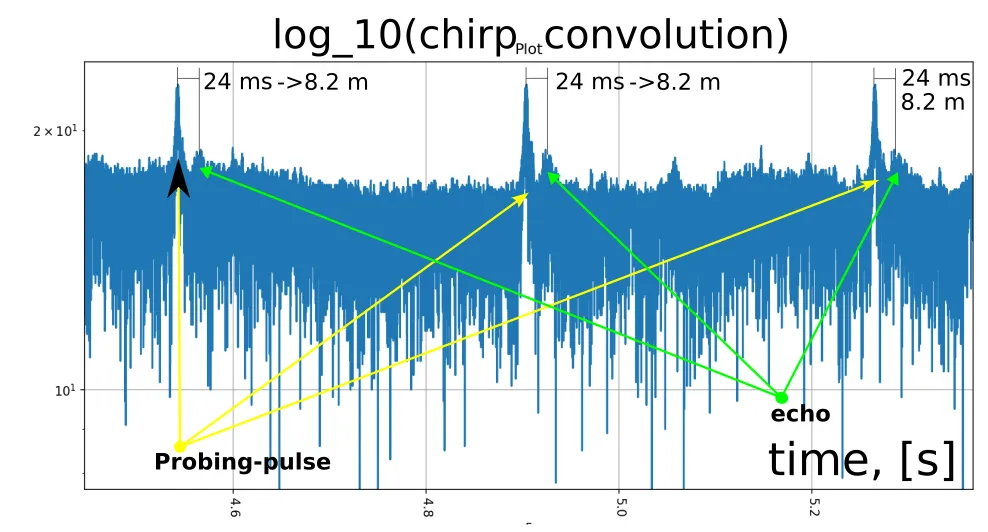
The echo is especially noticeable in the logarithmic scale on the Y-axis.

In the logarithmic scale, the maxima of the correlation of the recorded signal with the local copy of the LFM are more clearly visible.

At a distance of 4 meters, there was indeed a gate wall.

This is the next experiment. Here, the X-axis time is immediately recalculated into the distance to the target according to formula (1). That is, it is multiplied by the coefficient 331*0.5=165.5 [m]/[s]. On the Y-axis is the convolution result.

High reproducibility of the echo signal is noticeable. At first glance, it looks somewhat similar to the truth.

What can be improved?

1--Increase the sampling rate to 96kHz. This will improve the distance measurement resolution.

2--Increase the duration of the LFM signal. This will likely give a larger convolution maximum, as there will be more terms.

3--Record the echo on a matrix of three microphones in one horizontal plane. This way, it will be possible to determine the direction of the echo arrival and, thus, calculate the distance to objects with reference to the azimuth (bearing).

4--Calculate the convolution in real-time on the FPGA. This will increase the efficiency of the sonar.

5--By measuring the echo in known locations, for example along a line, it is possible to numerically construct a map of the surrounding space. In acoustics, the same methods and signal processing algorithms can be applied as in synthetic aperture radar (SAR/RCA).

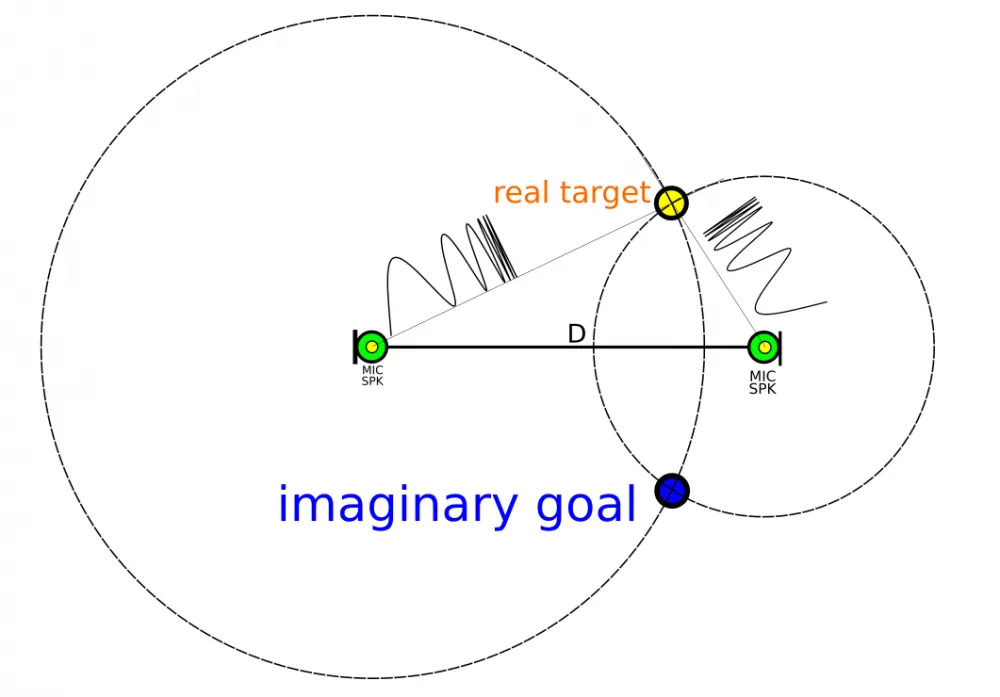
How to find local maxima in the convolution graph? Very simple. You can program a filter that will look for maxima in a sliding window. This will result in an array of possible targets. At the same time, a separate microphone does not know from which azimuth these echoes came. Therefore, it is necessary to build concentric circles of target locations around each microphone. The intersections of these circles will indicate the target coordinates.

For example, thanks to echo measurements from just two known coordinates along a line at a distance D, it is possible to determine the target coordinates with an accuracy of up to a mirror image.

Results

It was practically confirmed that making a sonar from an ordinary telephone audio codec is a feasible task. It's just a matter of calculations. The LFM signal can serve as a probing pulse.

The FIR filter can be used to calculate the convolution by simply writing the function with the filter coefficients.

Such sound experiments can be conducted as laboratory work in universities for digital signal processing, radar, and hydroacoustics.

Glossary

Questions

Are there hardware-configurable FIR filter chips (in ASIC implementation)?