How to prove Einstein's theory of relativity for $100

The same is done by photons, particles of light. Some of these particles are particularly energetic and can knock electrons off atoms and molecules to which they are usually bound, creating free electrons and ions that can also collide with you. Ghostly neutrinos and antineutrinos pass through your body, although they rarely interact with you. But much more happens to your body than you think.

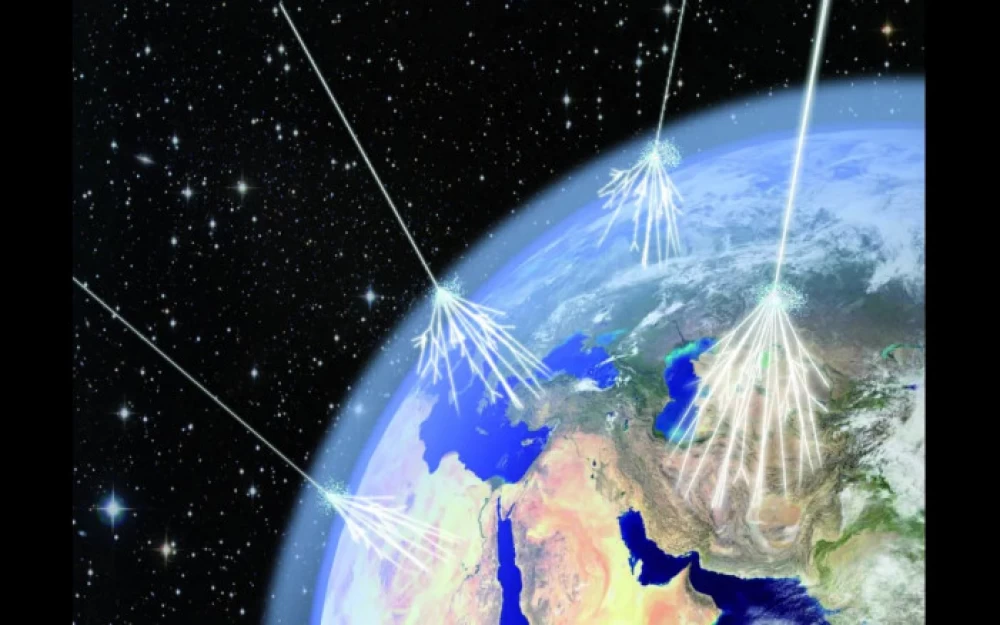
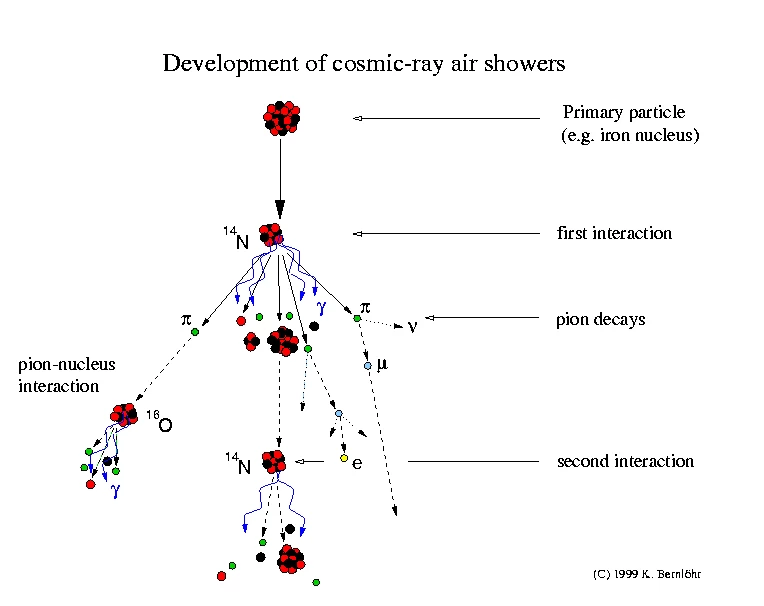
Throughout the Universe, from stars, black holes, galaxies, etc., cosmic rays are emitted - particles rushing through the Universe with high energies. They enter the Earth's atmosphere and cause showers of both stable and unstable particles. Those of them that live long enough before decaying eventually reach the Earth's surface. Every second, 10 to 100 muons - unstable, heavy cousins of the electron - pass through your body. With an average lifetime of 2.2 microseconds, you might think they couldn't travel the entire thickness of the atmosphere, ~100 plus kilometers, from space to your hand. Nevertheless, the theory of relativity asserts that this happens, and the fact that these muons pass through your body is more than enough to prove it right.

Individual subatomic particles are almost always invisible to the human eye, as the wavelengths of light we can see are not affected by particles passing through our bodies. But if you create pure vapor consisting of 100% alcohol, a charged particle passing through it will leave a trail that can be visually detected even by such a primitive device as the human eye. That's right: with a bit of chemistry, your own human eye can serve as a particle detector.

When a charged particle passes through alcohol vapor, it ionizes a track of alcohol particles that serve as centers for the condensation of alcohol droplets. The resulting trail is long and persistent enough for the human eye to see, and by the speed and curvature of the trail (if a magnetic field is applied), it is even possible to determine what type of particle it was.

This principle was first applied in particle physics using a cloud chamber (Wilson chamber).

Today, anyone can build a cloud chamber from readily available materials, spending one day of labor and less than $100 on parts. Particles moving in the atmosphere do not leave a visible trail, but particles moving in 100% pure alcohol vapors do! Alcohol particles serve as condensation centers, and when a charged particle passes through alcohol vapors (such as ethyl or isopropyl alcohol), it ionizes a track of these particles. As a result, a trail is formed that is large and long enough for your eyes to easily notice.

Building a cloud chamber is very simple, requiring only a few simple materials and actions:

Materials:

• A clear plastic or glass tub (e.g., an aquarium) with a sturdy lid (plastic or metal);

• Felt;

• Isopropyl alcohol (90% or more. You can find it at a pharmacy or order it from a chemical supply company. Wear safety goggles when working with alcohol);

• Dry ice (frozen carbon dioxide. Often used at fish markets and grocery stores to cool products. Wear thick gloves when handling dry ice).

Steps:

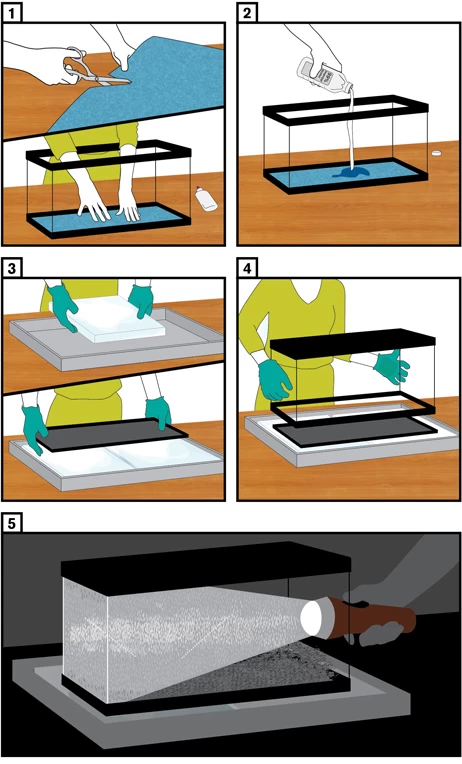
• Cut a piece of felt so that it is the size of the bottom of the aquarium. Glue it inside the aquarium (at the bottom, where the sand and fake treasure chests usually are).

• Once the felt is secured, soak it with isopropyl alcohol until it is saturated. Drain off the excess alcohol.

• Place the lid on dry ice so that it lies flat. You may want to place the dry ice in a container or box to make it more stable.

• Turn the container upside down so that the bottom of the container, covered with felt, is on top, and place the neck of the container on the lid.

• Wait about 10 minutes... then turn off the light and shine a flashlight into the container.

When a particle passes through your cloud chamber, it collides with molecules in the atmosphere and knocks some of their electrons off, turning the molecules into charged ions. The atmospheric alcohol is attracted to these ions and sticks to them, forming tiny droplets.

The trails left behind are similar to airplane contrails — long spindle-shaped lines marking the particle's path through the cloud chamber.

Many different types of particles can pass through your cloud chamber. It may be hard to notice, but you can actually distinguish the types of particles by the trails they leave behind.

Short, thick trails

Sorry, but this is not a cosmic ray. When you see short, thick tracks, it is a radon atom in the atmosphere spitting out an alpha particle (a clump of two protons and two neutrons). Radon is a naturally occurring radioactive element, but it is present in the air at such low concentrations that it is less radioactive than peanut butter. Alpha particles emitted from radon atoms are bulky and low-energy, so they leave short, fat tracks.

Long, straight tracks

Congratulations! You have muons! Muons are heavier cousins of the electron, they are formed when a cosmic ray collides with atmospheric molecules high in the atmosphere. Thanks to their mass, muons punch their way through the air and leave clean, straight tracks.

Zigzags and squiggles

If your track looks like the path of a lost tourist in a foreign city, you have an electron or positron (the antimatter twin of the electron). Electrons and positrons are formed when cosmic rays crash into atmospheric molecules. Electrons and positrons are light particles, and when they collide with air molecules, they scatter, leaving zigzags and squiggles.

Branching tracks

If your track splits, congratulations! You have just seen a particle decay. Many particles are unstable and decay into more stable ones. If your track suddenly splits, you have seen physics in action!

To ensure its functionality, I always recommend disassembling an old smoke detector and removing the mantle: the metal component that warns you of the presence of radioactive materials inside, usually an americium isotope. Since all americium isotopes decay, including americium-241 used in smoke detectors, they will emit particles capable of creating these ionization tracks. Place this mantle at the bottom of your cloud chamber, and once it is activated by performing the above steps, you will see particles emanating from it in all directions and leaving tracks in your cloud chamber.

Americium, in particular, decays by emitting α-particles. In physics, α-particles consist of two protons and two neutrons: this is the same as the helium-4 nucleus. Due to the low decay energy and large mass of α-particles, these particles take a slow, winding path, and sometimes you can see them bouncing off the bottom of the cloud chamber. This is a simple test to check if your cloud chamber is working correctly.

However, if you build a cloud chamber in this way, you will see not only the tracks of α-particles. In fact, even if you leave the chamber empty (i.e., do not place any source emitting particles inside or nearby), you will still see tracks: they will be mostly vertical and will look like perfectly straight lines.

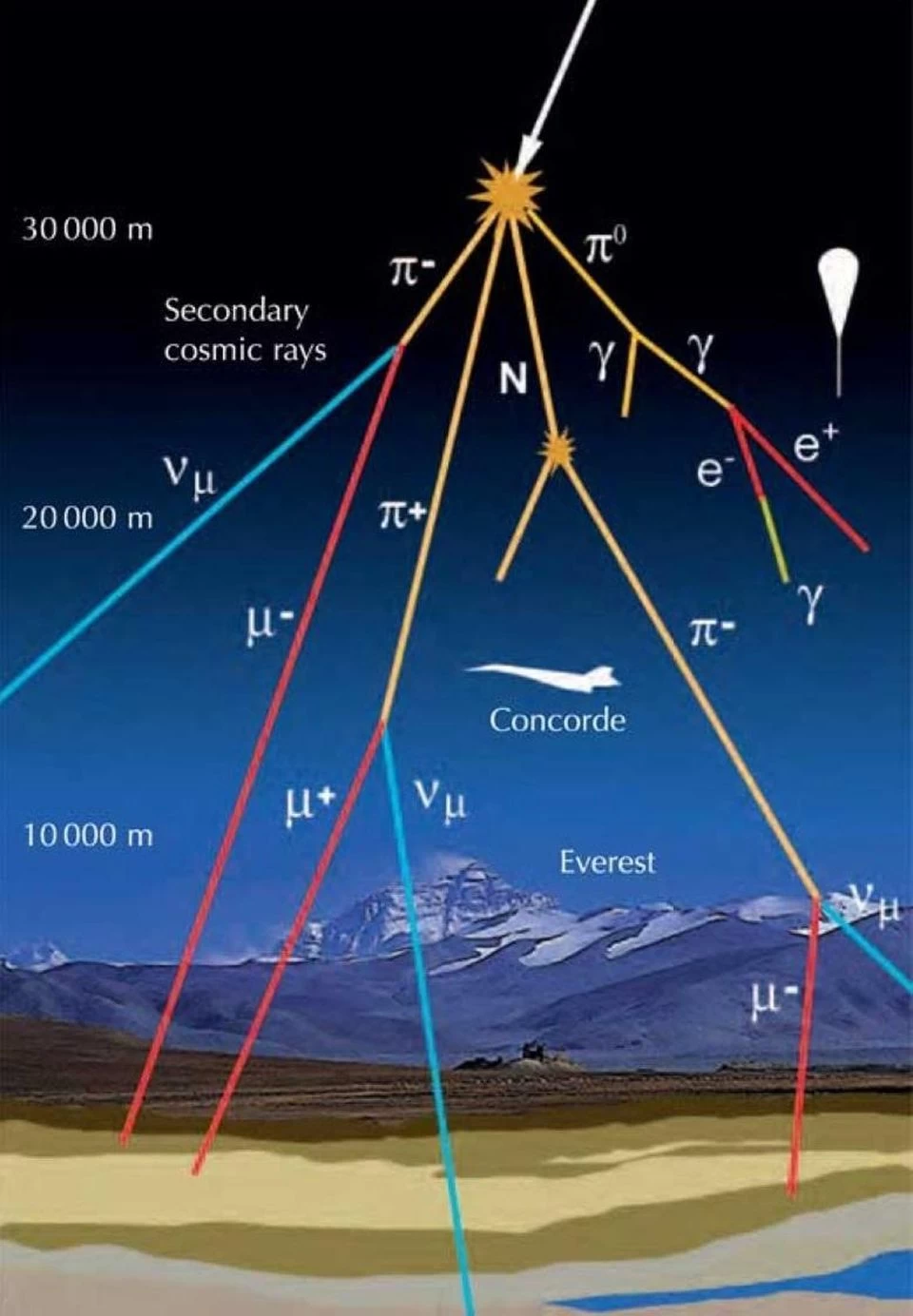
This is not due to radioactivity, but rather due to cosmic rays: high-energy particles that hit the upper part of the Earth's atmosphere, creating cascades of particles falling from top to bottom. Most cosmic rays hitting the Earth's atmosphere consist of protons, but they move at various speeds and energies. Higher energy particles collide with particles in the upper layers of the atmosphere, forming protons, electrons, and photons, as well as unstable, short-lived particles such as pions.

These particle showers are a hallmark of fixed-target particle physics experiments, and they also occur naturally as a result of cosmic rays.

Pions, consisting of a quark-antiquark combination, are unstable and come in three types:

• π+ — a positively charged pion, which lives for about 10 nanoseconds,

• π-, a negatively charged pion, which also lives for about 10 nanoseconds,

• and π0 — a neutral pion, which lives for a very short time, only about 0.1 femtoseconds.

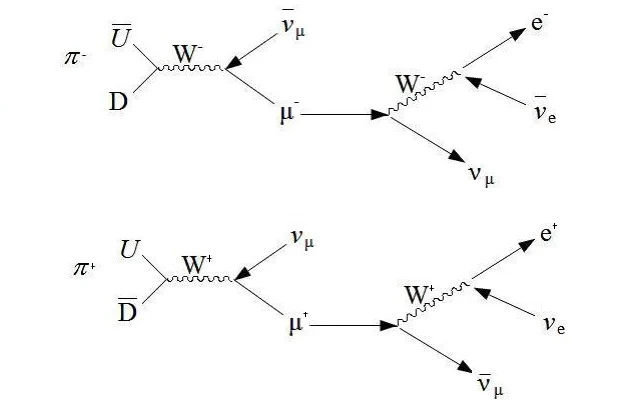
While neutral pions simply decay into two photons, charged pions primarily decay into muons of the same charge (in addition to neutrinos/antineutrinos). Muons are point-like particles, like electrons, but their mass is 206 times greater than that of an electron, and they are themselves unstable.

However, muons are not as unstable as the composite pion. In fact, muons are the longest-lived unstable fundamental particle known to us. Due to their relatively small mass, they live on average an astonishingly long 2.2 microseconds.

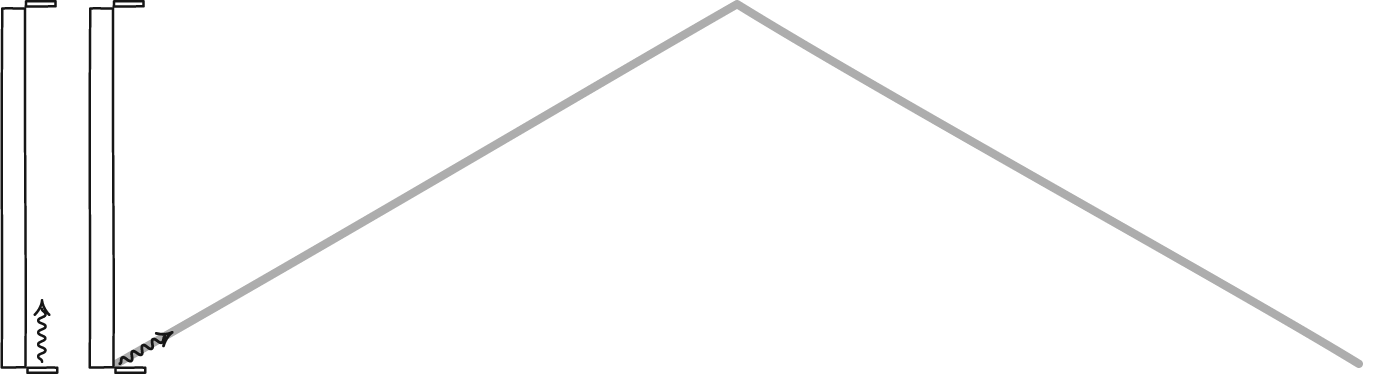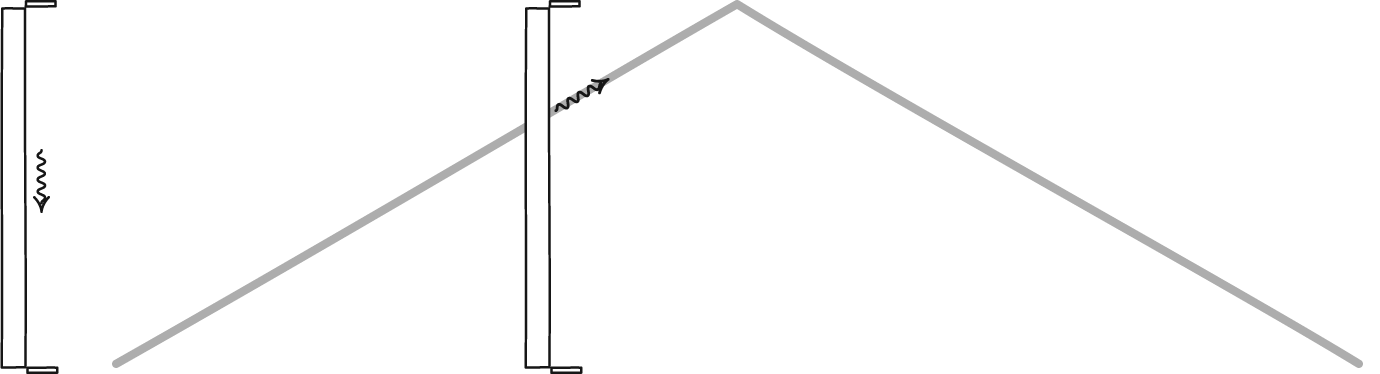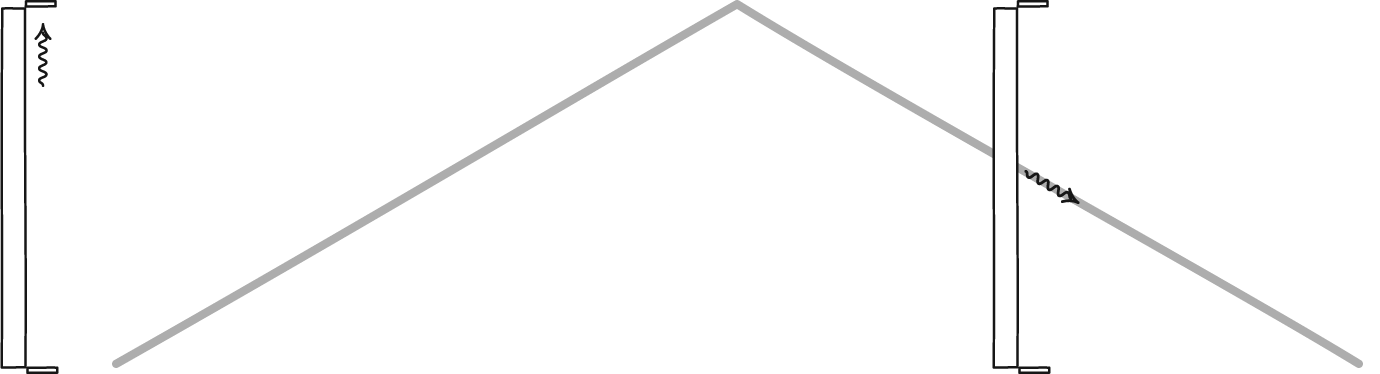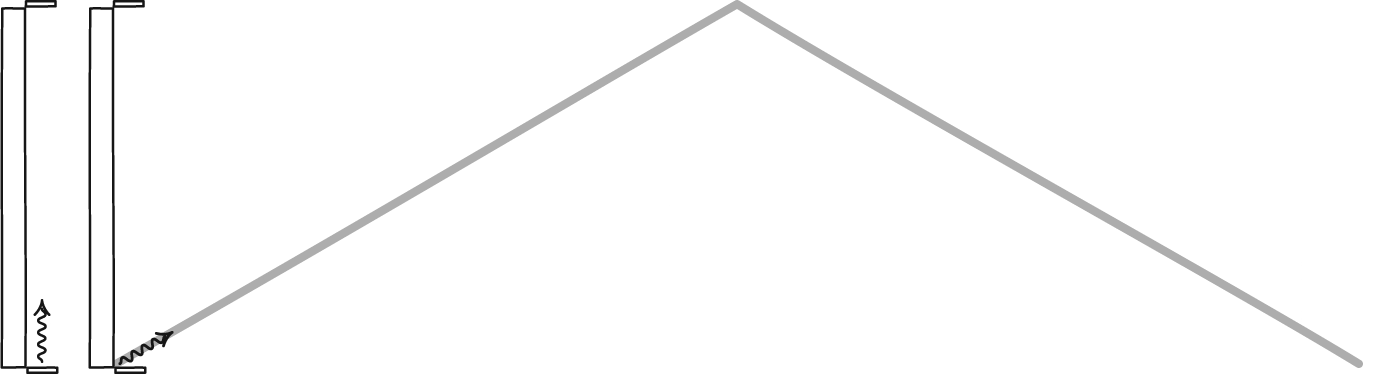
If you were to ask yourself what distance a muon can travel after its creation, you might think that you need to multiply its lifetime (2.2 microseconds) by the speed of light (300,000 km/s), which would give an answer of 660 meters. But then the question arises: why do you see them in your cloud chamber?

The Earth's atmosphere is more than 100 kilometers high, and although it is very rarefied at the highest altitudes, there are still more than enough particles in it to ensure rapid interaction with any incoming cosmic ray. These muons are created at a distance of 100 kilometers from the Earth's surface (or more) and have an average lifetime of only 2.2 microseconds. Here's the puzzle: if muons can live only 2.2 microseconds, their time is limited by the speed of light, and they are created in the upper layers of the atmosphere (at an altitude of about 100 km), then how can these muons reach us here on the Earth's surface?

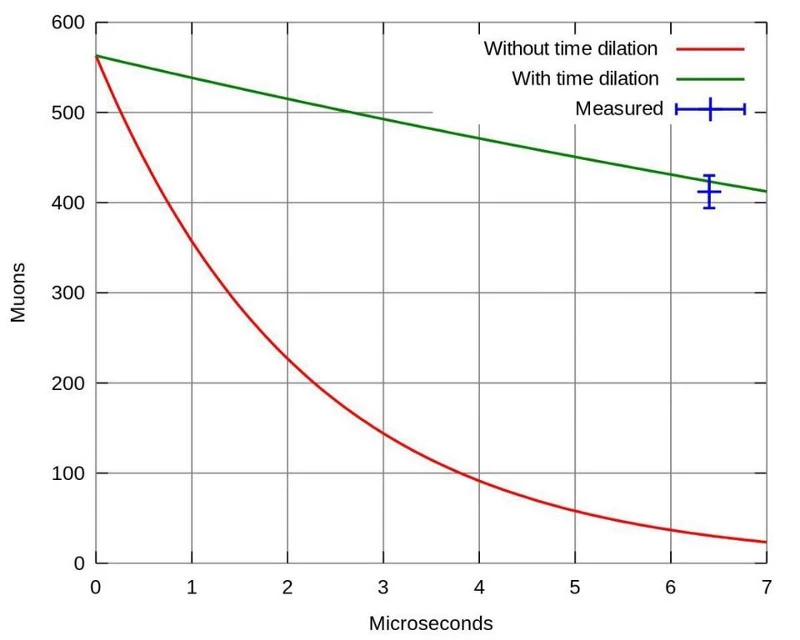
You can start making excuses. You can imagine that some cosmic rays have enough energy to continue cascading and creating particle showers all the way to the ground, but this is not the story that muons tell when we measure their energy: the lowest of them are still created at an altitude of about 30 km. You might think that 2.2 microseconds is just an average value, and perhaps rare muons living 3-4 times longer will have time to descend. But if you calculate, only 1 out of 10^50 muons should reach the Earth's surface without decaying; in reality, almost 100% of muons reach the Earth.

How can this discrepancy be explained? Of course, muons move at a speed close to the speed of light, but we observe them from a frame of reference in which we are stationary. We can measure the distance that muons travel, we can measure their lifetime, and even if we give them reason to doubt and say that they are moving at the speed of light (and not near it), they should not travel even 1 kilometer before decaying.

But this misses one of the key points of the theory of relativity!

Unstable particles do not experience time as you, the external observer, measure it. They experience time according to their own internal clocks, which will run slower the closer they are to the speed of light. Time slows down for them, which means that we will observe them living longer than 2.2 microseconds from our frame of reference. The faster they move, the further their visible path will be.

How does this work for the muon?

In its frame of reference, time runs normally, so by its internal clock, it will live only 2.2 microseconds. But it will perceive reality as if it is rushing towards the Earth's surface at a speed extremely close to the speed of light, causing length to contract along the direction of motion. Suddenly, it will have to cover not 100 kilometers to the Earth's surface, but the entire "proper distance" shortened by the Lorentz-Fitzgerald contraction.

If, for example, a muon is moving at 99.999% of the speed of light, then every 660 meters outside its frame of reference will look as if their length is only 3 meters: its own length decreases by 99.5%. A journey of 100 km down to the surface will look like a journey of 450 meters in the muon's frame of reference. According to the muon's own clock, a muon that appeared at an altitude of 100 km and was flying at such a speed would have lived only 1.5 microseconds of time. With such a small amount of lived time, the probability that each muon will decay during this journey is less than 1/2.

This allows us to understand how to reconcile the situation with the muon: from our frame of reference on Earth, we see that the muon travels 100 km in about 4.5 milliseconds. However, this is not a paradox, because the muon does not feel that 4.5 milliseconds have passed; this amount of time passes only in our frame of reference. According to the muon, the time it lives stretches relative to us, just as the length contracts relative to our length. From the muon's point of view, it traveled 450 meters in 1.5 microseconds, and therefore it can remain itself all the way to the end point - the surface of the Earth.

Without Einstein's laws of relativity, this cannot be explained!

However, in the context of relativity theory, high speeds correspond to high particle energies. The combined effect of time dilation and length contraction allows not just a few, but most of the created muons to survive. That's why even here, on the surface of the Earth, between 10 and 100 muons pass through your body every second. In fact, if you extend your hand and point it to the sky, about one muon per second will pass through this modest part of your body.

If you ever doubted the theory of relativity, it's hard to blame you: the theory itself seems so illogical, and its effects are beyond our everyday experience. But there is an experimental test that can be done at home, inexpensively and in just one day, that will allow you to see the effect firsthand.

You can build a cloud chamber, and if you do, you will see these muons. If you add a magnetic field to the setup, you will see the muon tracks bend according to their charge-to-mass ratio: you will immediately understand that these are not electrons. In rare cases, you could even see a muon decay in the air. And finally, if you measured their energy, you would find that they move ultra-relativistically, at 99.999% the speed of light. If it weren't for relativity, you wouldn't see a single muon at all.

Time dilation and length contraction are real, and the fact that muons survive, reaching the Earth's surface in cosmic ray showers, proves this beyond a shadow of a doubt.